Сферический осциллятор, кулоновский потенциал и бесконечно глубокая сферическая потенциальная яма 4 страница

А.

Б.

В.

−1

Г.

−1

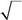
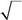
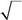
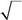555. Спин частицы равен½.Какая из нижеприведенных матрицявляется матрицей оператора s ˆ _y в s_z -представлении?

А.	1				Б.	1
		−1 0			−1
В.	1		0 − i	Г.	1	− i
							i
	^i

556. Спин частицы равен½.Оператор квадрата проекции спина наось y равен

А.

1

0 1

Б.

1

В.

1

−1

^1 0

−1

Г.

1

^0

^1

557. Спин частицы равен½.Какие из перечисленных функций яв-ляются собственными функциями оператора s ˆ _y ²?

А. только		и		Б. только	и
		^1		^1	− 1
			Г. все двухкомпонентные столбцы
В. только		и
^i	^− ^i

558. Какая из четырех нижеперечисленных матриц является однойиз матриц Паули?

	0 1	i		0 − i	0 i
А.	−1 0		Б.			В.			Г.
			− i	i		i 0

559. Какая из четырех нижеперечисленных матриц является матри-цей Паули σ_z?

А.

0 1

Б.

В.

0 − i

Г.

0 i

−1 0

^0

−1

i

i 0

560.Какая матрица отвечает оператору s ˆ xs ˆ y − s ˆ ys ˆ x?

А.

1

i 0

Б.

1

0 i

В.

1

i

Г.

1

0 i

− i 0

0 i

^0

− i

^i

561. Из четырех нижеприведенных спиновых функций только однаявляется собственной функцией оператора s ˆ _x. Какая?

			i
А. ψ (sz) =		Б. ψ (sz) =
			^1
В. ψ (sz) =	Г. ψ (sz) =
	−1	^0

562. Из четырех нижеприведенных состояний только в одном вели-чина s_x имеет определенное значение. В каком?

А. ψ (sz) =	Б. ψ (sz) =
		^2
В. ψ (sz) =	Г. ψ (sz) =
		^1

563. Какая из нижеперечисленных функций является собственнойфункцией оператора s ˆ _y?

		− i
А. ψ (sz) =	Б. ψ (sz) =	В. ψ (sz) =
^i		i		−1

1 ^{Г. ψ ( s}z ⁾⁼₁

564. Чему равно среднее значение проекции спина на ось x в со-

^{стоянии ψ ( s}z ⁾⁼₁^?

А. s_x = −1/ 4 Б. s_x =1/ 4 В. s_x =1/ 3 Г. s_x = 0

565. Чему равно среднее значение проекции спина на ось x в со-

		/ 2
стоянии ψ (sz) =	1/		?
А. sx = 3 / 8		Б. sx = − 3 / 8	В. sx = 3 / 4
Г. sx = − 3 / 4

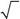
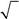
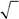
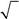
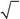566. Чему равно среднее значение проекции спина на ось y в со-стоянии

ψ (s_z)=^{1 1}?

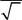
2 1

А. s_y = −1/ 4 Б. s_y =1/ 4 В. s_y =1/ 3 Г. s_y = 0

567. В результате действия на спиновую волновую функцию

ψ (s_z) = ₂ оператора s ˆ _x получится следующая спиновая волно-

вая функция
А. ψ (sz) =			Б. ψ (sz) =
1/ 2		1/ 4
В. ψ (sz) =		Г. ψ (sz) =
568.В результате	действия на спиновую	волновую функцию

ψ (s_z) = ₂ оператора s ˆ _y получится следующая спиновая волно-

вая функция:

А. ψ (s_z)

Г. ψ (s_z)

− i

⁼ i / 2 i / 2

⁼ − i

	i			− i / 2
Б. ψ (sz) =	− i / 2		В. ψ (sz) =	i

569. Спин частицы равен½.Какая матрица отвечает оператору s ˆ _x s ˆ _y + s ˆ _y s ˆ _x?

i 0

А.

Б.

В.

Г.

0 i

^1

570. Какое утверждение относительно свойств оператора s ˆ _xs ˆ _y яв-

ляется верным?

А. он неэрмитов Б. он унитарен

В. он совпадает со своим обратным Г. он нелинеен

571. Спиновая функция частицы имеет вид ψ (s_z)=₀.Будет ли

это состояние стационарным? А. да Б. нет

В. мало информации, чтобы ответить

Г. зависит от того, коммутирует ли оператор s ˆ _y с оператором Га-

мильтона или нет 572. Частица имеет спин½.Гамильтониан частицы не зависит от

спиновых переменных. Оператор какого вида отвечает гамильто-ниану?

ˆ	ˆ				ˆ	ˆ
А. H (r, s z) = h (r)			Б. H (r, s z) = h (r)
			^1			^1	^1
ˆ	ˆ				ˆ	ˆ	0 1
В. H (r, s z) = h (r)			Г. H (r, s z) = h (r)
			−1			^1 0

^ˆ действует на пространственные переменные) (где оператор h (r)

573. Частица имеет спин½.Гамильтониан частицы не зависит отспиновых переменных. Какой функцией описывается спиновая часть собственных функций гамильтониана?

				В. никакой из них
А. только			Б. только

Г. любой линейной комбинацией функций А и Б

ГЛАВА 6. КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ

574. Квазиклассическое приближение–этоА. метод перехода от квантовой механики к механике классической

Б. приближение, в котором оператор импульса заменяется на им-пульс В. метод приближенного решения стационарного уравнения Шре-

дингера, основанный на «плавности» потенциала как функции ко-ординаты Г. метод приближенного решения временного уравнения Шредин-

гера, основанный на «плавности» волновой функции системы как функции времени

575. Чтобы квазиклассическое приближение работало, нужно что-

бы А. потенциальная энергия была резкой функцией координаты

Б. потенциальная энергия была плавной функцией координаты В. потенциальная энергия была большой Г. потенциальная энергия была маленькой

576. Какой из нижеследующих формул определяется параметр ква-

зиклассичности? (k (x) =

2 m E − U (x) /

^2, m – масса частицы)

k ′(x)

Б.

k ^2(x)

В.

k ′(x)

Г.

k ^3(x)

А.

k

(x)

′

k

(x)

′

k (x)

k (x)

577. Какова размерность

| k ′(x) / k ² (x) |?

А. длина Б. _длина¹

Г. безразмерный

578. График зависимости потен-циальной энергии от координаты приведен на рисунке. В какой

точке – x ₁ или x ₂ – лучше рабо-

тает квазиклассическое прибли-жение?

А. в точке x ₁

параметра квазиклассичности

^В. _длина2

U (x)

^x 1 ^x 2

x

Б. в точке x ₂

В. по рисунку это определить невозможно Г. это зависит от энергии, при которой решается уравнение Шре-дингера

579. Условие применимости квазиклассического приближения час-

то записывают в виде	d λ (x)	1. Что означает здесь λ (x)?
dx

А. это длина волны света, который излучает частица в точке с ко-ординатой x

Б. это длина волны света, который имеет ту же энергию, что и час-тица в точке с координатой x

В. λ (x) = _{p ( x )} = _{2 m ( E − U ( x ))} – де-бройлевская длина волны

частицы, выраженная через классический импульс в точке с коор-динатой x

Г. λ (x) = ^{p ( x )} = ^{2 m ( E − U ( x ))} – де-бройлевская длина волны

частицы, выраженная через классический импульс в точке с коор-динатой x

580.График потенциальной энер-	U (x)
гии частицы имеет вид, показан-	E 2
ный на рисунке. Уравнение Шре-
дингера решается при двух энер-	E 1		x

гиях – E ₁ и E ₂ (показаны на ри-

сунке). При какой энергии лучше работает квазиклассическое при-

ближение?
А. лучше при энергии E 1	Б. лучше при энергии E 2
В. безразлично			U (x)
Г. от энергии точность квазиклас-	E
сического приближения не зависит			x
581.Решается уравнение Шредин-
гера при некоторой энергии E (по-
казана на рисунке) в двух потен-
циалах, графики которых показаны

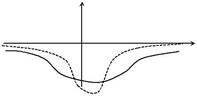
на рисунке (один потенциал – сплошной линией, второй – пункти-ром). Для какого потенциала – «сплошного» или «пунктирного» – лучше работает квазиклассическое приближение?

А. лучше для «сплошного» Б. лучше для «пунктирного»

В. одинаково Г. зависит от энергии

582. Уравнение Шредингера решается в окрестности точки,в кото-рой вторая производная потенциала равна нулю V ′′(x) = 0. Что

можно сказать о возможностях квазиклассического приближения в этой области?

А. оно хорошо работает Б. оно плохо работает В. точность квазиклассического приближения не связана со второй производной потенциала Г. не работает никогда

583. Уравнение Шредингера решается в окрестности точки,в кото-рой потенциал имеет максимум, при энергии, отличающейся от значения потенциала в точке максимума. Что можно сказать о воз-можностях квазиклассического приближения в этой области?

А. оно хорошо работает Б. оно плохо работает В. точность квазиклассического приближения не связана с макси-мальностью потенциала Г. не работает никогда

584. Частица движется в потенциале U (x)= U ₀= const. Чему рав-но значение параметра квазиклассичности для этой частицы?

А. 0	Б.	U 0		В. ∞	Г.	U 0 − E
E
					U 0
(E – энергия частицы)			α
585.	Частица движется в потенциале U (x) =	(α < 0). Каким
x ^2

является параметр квазиклассичности при нулевой энергии части-цы?

Дата добавления: 2014-12-24