Сферический осциллятор, кулоновский потенциал и бесконечно глубокая сферическая потенциальная яма 3 страница

ψ 1			и ψ 2		i
(sz) =			(sz) =		?
	^i				− 2 i

А. − i + 2 Б. i + 2 В. i − 2 Г. − i − 2

532. Дана спиновая волновая функция некоторого состояния час-тицы

	i / 3
	2 / 3 − 2 i / 3		. Что можно сказать о нормировке этой
ψ (s z)=
функции?
А. она нормирована на 1	Б. она нормирована на 2
В. она нормирована на 3	Г. она нормирована на 9
533.Частица находится в	состоянии с волновой функцией

ψ (s			−3 i / 11
z	) =		. Будет ли квадрат проекции спина на ось z
		2 /11

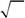
иметь определенное значение в этом состоянии?

А. да Б. нет В. зависит от способа измерений Г. недостаточно информации, чтобы ответить

534. Частица находится в состоянии с волновой функцией

	−1/ 2
ψ (s z)=		. Будет ли квадрат проекции спина на ось z
i	3 / 2

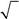иметь определенное значение в этом состоянии?

А. да Б. нет В. зависит от способа измерений Г. недостаточно информации, чтобы ответить 535. Частица находится в состоянии с волновой функцией

	−1/
ψ (s z)= i /	. Будет ли квадрат проекции спина на ось z

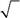
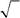иметь определенное значение в этом состоянии?

А. да Б. нет В. зависит от способа измерений Г. недостаточно информации, чтобы ответить

536. Частица со спином s =1находится в состоянии со спиновойфункцией

				1/
									в этом состоянии.
ψ (s z)=1/	. Найти sz
				1/
А. sz ^2 =1/ 3					Б. sz ^2	= 2 / 3
В. sz ^2 =1/ 6					Г. sz ^2	= 5 / 6

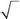
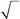
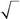537. Спин частицы равен1/2.Чему равны собственные значенияоператора проекции спина на ось y?

А. +1 и −1 Б. +1/ 2 и −1/ 2

В. +1, 0 и −1 Г. +3/ 2, +1/ 2, −1/ 2 и −3/ 2

538. Частица со спином1/2находится в состоянии,в котором про-екция ее спина на ось z с вероятностью 1/4 принимает значение 1/2 и с вероятностью 3/4 – значение –1/2. Какой функцией не может описываться состояние такой частицы?

−1/ 2

Б. ψ (sz) =

− i 3 / 2

А. ψ (sz) =

3 / 2

1/ 2

^i

В. ψ (sz) =

Г. ψ (sz) =

− 1

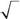
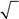
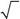
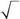539. Какая матрица(матрицы)отвечает эрмитовому оператору?

1 0

0 1

В.

0 0

0 0

А.

Б.

Г.

0 0

0 0

0 1

1 0

540.Какая матрица(матрицы)отвечает эрмитовому оператору?

i 0

0 i

В.

i

0 i

А.

Б.

− i 0

Г.

0 i

^0

− i

i 0

541.Коммутатор[ s ˆ x, s ˆ z ]

равен

А. is ˆ x

Б. is ˆ y

В. − is ˆ y

Г. s ˆ^2

542.Какой из перечисленных коммутаторов равен нулю?

А. только

s ˆ^2

, s ˆ

Б. только

s ˆ^2

, s ˆ

Г. только

s ˆ^2

, s ˆ

−

+

^z

Г. все перечисленные

543. Выбрать верное равенство

А. [ s ˆ₊, s ˆ₋ ] = 2 s ˆ _x Б. [ s ˆ₊, s ˆ₋ ] = 2 s ˆ _y

В. [ s ˆ₊, s ˆ₋ ] = 2 s ˆ _z Г. [ s ˆ₊, s ˆ₋ ]= 2 s ˆ²

(где s ˆ_± = s ˆ _x ± is ˆ _y – повышающий и понижающий проекцию спина

частицы на ось z операторы)

544. Спин частицы равен1.Какая матрица отвечает оператору s ˆ _z в

sz -представлении?
А.	^1		Б.
В.		Г.
	−1

545. Спин частицы равен3/2.Какая матрица отвечает оператору s ˆ _z

в sz -представлении?
												0 0
									1				0 0
А.			Б.
											−1 0
													0 −3
	1								1
В.			Г.

546. Спин частицы равен100.Какой является матрица оператора

s ˆ _z?

А. диагональной, размерности 100 ×100, на диагонали числа

100, 99,...,1

Б. диагональной, размерности 101 ×101, на диагонали

числа

100, 99,..., 0

В.

диагональной,

размерности

200 ×200,

на

диагонали

числа

100, 99,..., − 99, −100

Г.

диагональной,

размерности

201 ×201,

на

диагонали

числа

100, 99,..., − 99, −100

547.Спин частицы равен1/2.Матрица оператора s ˆ^2–это

А.

3

1 0

Б.

3

1 0

В.

1

1 0

0 1

−1

0 −1

Г.

1

548. Какая функция получится в результате действия оператора s ˆ²

на спиновую волновую функцию ψ (sz) =		^?
	3/ 4		3/ 4
А. ψ (sz) =		Б. ψ (sz) =
	− 6 / 4		6 / 4
	− 3/ 4		−3 / 4
В. ψ (sz) =		Г. ψ (sz) =	− 6 / 4
	6 / 4

549. Спин частицы равен1.Матрица оператора s ˆ²–это

А.			Б.
В.		Г.
	−1

550. Спин частицы равен3/2.Матрица оператора s ˆ²–это

									3 0 0 0
А.	9						Б.	15		0 1 0 0
								0 0 −1 0
											0 0 0 −3
В.	15					Г.	9
										−1 0
													−3

551. Какая из четырех нижеприведенных матриц отвечает операто-ру s ˆ₊?

А.

Б.

В.

Г.

552. Какая из четырех нижеприведенных матриц отвечает операто-ру s ˆ₋?

А.

Б.

В.

Г.

553. Какая функция поучается в результате действия оператора,повышающего проекцию спина частицы на ось z, на спиновую

^{функцию ψ ( s}z ⁾⁼₀^?

А. ψ (sz) =		Б. ψ (sz) ∼	В. ψ (sz) ∼
								^1
Г. ψ (sz) ∼
								действии оператора s ˆ+ на
554.Какая	функция	получится при
функцию ψ (sz) =					?

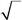
Дата добавления: 2014-12-24