Свойства собственных значений и собственных функций операторов момента импульса

350. Какие из нижеследующих чисел исчерпывают все собственныезначения оператора квадрата орбитального момента импульса?

А.	2 l 2	Б. ^2 l (l +1)	В.	^2 l (l +2)	Г. ^2 l (l −1)
(l – целое неотрицательное число)
351.	Собственными значениями оператора квадрата орбитального
момента импульса являются числа вида	^2 l (l +1),где l
А. полуцелое неотрицательное число (число вида 1/2, 3/2, …)
Б. целое неотрицательное число
В. целое неположительное число
Г. полуцелое неположительное число
352.	В некотором состоянии квадрат орбитального момента им-

пульса частицы принимает определенное значение: L ² =12 ². Ка-кую из перечисленных величин принято называть величиной мо-мента в этом состоянии?

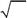
А. 3 Б. 4 В. 12 Г. − 12 353. Какие из нижеследующих чисел исчерпывают все собственныезначения оператора проекции орбитального момента импульса на ось z?

А. m (m – любое целое или полуцелое число)

Б. m (m – любое целое положительное число)

В. m (m – любое целое отрицательное число)

Г. m (m – любое целое число)

354. Какие из нижеследующих чисел исчерпывают все собственныезначения оператора проекции орбитального момента импульса на ось x?

А. m (m – любое целое или полуцелое число)

Б. m (m – любое целое положительное число)

В. m (m – любое целое отрицательное число)

Г. m (m – любое целое число)

355. Частица находится в состоянии с определенной проекцией ор-битального момента на ось y: L_y = 4. Измеряют квадрат момен-

L ²=30

та импульса. Какое из перечисленных значений не могло быть при этом получено?

А. 24 ² Б. 30 ² В. 42 ² Г. 20 ²

356. Частица находится в состоянии с определенной проекцией ор-битального момента импульса на ось y: L_y = 4. Измеряют квад-

рат орбитального момента. Какое из перечисленных значений мог-ло быть при этом получено?

А. 49 ² Б. 36 ² В. 25 ² Г. 42 ²

357. Частица находится в состоянии с определенным значением

квадрата орбитального момента импульса: ². Измеряют

проекцию орбитального момента на ось	x. Какое из перечислен-
ных значений не могло быть при этом получено?
А. 5	Б. −4	В. 6	Г. 3

358. Какие из нижеследующих функций являются собственными

ˆ
для оператора Lz?		В. exp (imϕ)
А. sin mϕ	Б. exp(mϕ)

Г. cos mϕ (где m – любое целое число)

359. Какие из нижеследующих функций являются собственными

ˆ
для оператора Lz?		В. cos (mϑ + mϕ)
А. sin mϑ	Б. sin mϕ

Г. никакие

(m – любое целое число)

360. Частица находится в состоянии с одной из нижеследующихволновых функций:

А. sin ϕ Б. exp(− iϕ) В. exp(− iϑ)

Г. sin ϑ

В каких из этих состояний результат измерения проекции орби-тального момента на ось z не имеет определенного значения? 361. Частица находится в состоянии с волновой функциейsin mϑ,где m – некоторое целое число. Измеряют проекцию орбитального момента импульса частицы на ось z. Какие значения можно полу-чить и с какими вероятностями?

А. единственное значение L_z = m

Б. L_z = m и L_z = − m с вероятностями ½ В. единственное значение L_z = − m

Г. единственное значение L_z = 0

362. Какая из нижеследующих функций является общей собствен-

	ˆ
ной функцией операторов p ˆ z и Ly?
А. e iϕ eiky	Б. e iϕ e − iky	В. e − iϕe − iky
Г. такой функции не существует

(k – некоторое действительное число)

363. Какая из нижеследующих функций является общей собствен-

ной функцией операторов

ˆ

(k – некоторое действительное

p ˆ z и Lz

число, m – некоторое целое число)?

А. e − imϕe − ikz

Б. e − imϕe − ky

В.

e − mϕe − iky

Г. такой функции не существует

364.

Какая из

нижеследующих

функций является собственной

ˆ

функцией оператора Lz?

А.

x + iy

Б.

x +2 iy

В.

x −2 iy

x ^2+ y ^2

x ^2+ y ^2

x ^2+ y ^2

Г. в декартовых координатах записать эту функцию нельзя 365. Сферические функции–это

А. общие собственные функции операторов квадрата орбитального момента и его проекции на ось z

Б. общие собственные функции операторов квадрата орбитального момента и его проекции на ось x

В. общие собственные функции операторов квадрата орбитального момента и его проекции на ось y

Г. все перечисленные

366. Частица находится в состоянии с волновой функциейcos ϕ.

Измеряют проекцию орбитального момента на ось z. Какие значе-ния могут быть получены и с какими вероятностями?

А.		и 2		с вероятностями ½
Б.		и −		с вероятностями ½
В.		, и 2 с вероятностями 1/3
Г.	−	, 0	,	с вероятностями 1/3

367. Существует ли среди сферических функций такая функция(или функции), которая не зависит от полярного и азимутального углов ϑ и ϕ?

А. да Б. нет

В. существуют функции не зависящие от ϑ, но зависящие ϕ

Г. все сферические функции не зависят от углов, так как они обла-дают сферической симметрией 368. Частица находится в состоянии с волновой функцией

sin ϑ cos ϕ. Будут ли орбитальный момент и его проекция на ось z

иметь определенные значения в этом состоянии?
А. проекция – да, момент – нет
Б. проекция – нет, момент – да
В. и проекция, и момент
Г. ни момент, ни проекция.
369.	Частица	находится	в	состоянии	с	волновой	функцией
Y 54(ϑ, ϕ).Какие значения квадрата орбитального момента могут
быть получены при измерениях?
А. любое из чисел 0, 2 ^2,		^2, 12 ^2,	20 ^2, 30
Б. 20 ^2	В. 25 ^2			Г. 30 ^2
370.	Частица	находится	в	состоянии	с	волновой	функцией

Y ₅₄(ϑ, ϕ).Измеряют проекцию орбитального момента на ось z. Какие значения могут быть получены при измерениях?

А. m = 5	Б. любое целое число из интервала −4 ≤ m ≤ 4
В. m = 4	Г. любое целое число из интервала −5 ≤ m ≤ 5
371.Частица	находится в состоянии с волновой функцией

Y ₅₄(ϑ, ϕ).Измеряют проекцию орбитального момента на ось x. Какие значения могут быть получены при измерениях?

А. l_x = 5 Б. любое целое число из интервала −4 ≤ l _x ≤ 4

В. l_x = 4 Г. любое целое число из интервала −5 ≤ l _x ≤ 5

372. Частица находится в состоянии с волновой функцией

Y ₅₄(ϑ, ϕ).Какие значения орбитального момента и его проекциина ось z могут быть получены при измерениях?

А. l = 4, m = 5 Б. l = 5, m = 4 В. l = 4, m = −5

Г. никакие из перечисленных 373. Частица находится в состоянии с нормированной волновой

функцией C ₁ Y ₅₄ (ϑ, ϕ) + C ₂ Y ₅₃ (ϑ, ϕ), где C ₁ и C ₂ – числа. Какие значения орбитального момента можно обнаружить в этом состоя-нии и с какими вероятностями?

А. l = 5	с единичной вероятностью
Б. l = 3	с вероятностью | C		|^2	и l = 4	с вероятностью | C |^2
В. l = 5	с вероятностью | C |^2	+ | C		|^2	, l = 3 с вероятностью | C		|^2

и l = 4 с вероятностью | C ₁ |²

Г. l = 3 и l = 4 с одинаковыми вероятностями

374. Частица находится в состоянии с нормированной волновой

функцией C ₁ Y ₅₄ (ϑ, ϕ) + C ₂ Y ₅₃ (ϑ, ϕ), где C ₁ и C ₂ – числа. Какие значения проекции орбитального момента на ось z можно обна-ружить в этом состоянии и с какими вероятностями?

А.	m =5с единичной вероятностью
Б.	m =3	с вероятностью | C		|^2 и	m =4с вероятностью| C |^2
В.		m =5	с вероятностью	| C |^2	+ | C		|^2	,	m =3с вероятностью
| C		|^2 и m = 4 с вероятностью | C |^2
Г.	m =3	и m = 4 с одинаковыми вероятностями.
375.Частица находится	в состоянии		с волновой функцией

cos ² ϑ − 3cos ϑ +1. Измеряют проекцию орбитального момента на ось z. Какие значения можно при этом получить?

А. определенное значение m = 0 Б. определенное значение m = 2

В. любое значение из m = 0, 1, 2

Г. любое целое значение из интервала −2 ≤ m ≤ 2

376. Частица находится в состоянии с волновой функцией

cos ² ϑ − 3cos ϑ +1. Какие значения орбитального момента можно получить при измерениях в этом состоянии?

А. одно из чисел 0, 1, 2 Б. одно из чисел 0, 2

и m = 5 с вероятностью | C ₂ |²

В. одно из чисел −2, 0, 2 Г. одно из чисел

0, 1, 2, 3.

377. Частица находится в состоянии с нормированной волновой

функцией C ₁ Y ₆₃ (ϑ, ϕ) + C ₂ Y ₅₃ (ϑ, ϕ), где C ₁ и C ₂ – числа. Какие значения орбитального момента можно получить при измерениях в этом состоянии и с какими вероятностями?

А. l = 3 с единичной вероятностью

Б.	l =6	с вероятностью | C |^2	и l = 5	с вероятностью | C		|2
В.	l =3	с вероятностью | C |^2	+ | C		|2	, l = 6 с вероятностью | C |^2
и l = 5 с вероятностью | C 2 |^2
Г. l = 5	и l = 6 с одинаковыми вероятностями.

378. Частица находится в состоянии с нормированной волновой

функцией C ₁ Y ₆₃ (ϑ, ϕ) + C ₂ Y ₅₃ (ϑ, ϕ), где C ₁ и C ₂ – числа. Какие значения проекции орбитального момента на ось z можно полу-чить при измерениях в этом состоянии и с какими вероятностями? А. m = 3 с единичной вероятностью

Б. m = 6 с вероятностью | C ₁ |²

В. m = 3	с вероятностью | C |^2	+ | C		|2	,	m =6с вероятностью
| C |^2	и m = 5 с вероятностью | C		|2

Г. m = 5 и m = 6 с одинаковыми вероятностями.

379. Частица находится в состоянии,в котором ее орбитальныймомент импульса и его проекция на ось z имеют определенные значения: l =1, m = −1. Сравнить вероятности различных значе-

ний проекции момента на ось	y в этом состоянии: w (ly =1)и
w (ly = −1)
А. w (l y = 1) > w (ly = −1)	Б. w (l y =1) < w (ly = −1)
В. w (l y = 1) = w (ly = −1)

Г. такие значения проекции момента на ось y в данном состоянии

не могут быть обнаружены 380. Частица находится в состоянии,в котором проекция ее момен-

та импульса на ось z имеет определенное значение l _z = m. Изме-

ряют проекцию момента на ось y. Какие значения можно обнару-

жить?

А. l _y = m Б. любое целое число из интервала − m ≤ l _y ≤ m

В. l y = − m	ˆ
Г. любое собственное значение оператора Ly

381. Как сферическая функция Y_lm (ϑ, ϕ)зависит от азимутальногоугла ϕ?

А. как sin mϕ Б. как cos mϕ В. как e^imϕ

Г. как e ^{− imϕ}

382. Частица находится в состоянии с волновой функцией Y ₂₁(ϑ, ϕ).Проводят многократные измерения проекции орбиталь-ного момента импульса на ось y над ансамблем таких частиц. Ка-

кие значения будут получены?

А. l_y = 2 во всех опытах Б. l_y = −1, 0,1

В. l_y = −2, −1, 0,1, 2 Г. l_y =1 во всех опытах

383. Частица находится в состоянии с определенными значениямиорбитального момента l = 3 и его проекции на ось x l_x =1. Чему равно среднее значение проекции орбитального момента на ось z?

А.	lz	=1	Б.	lz	= 3
В.	lz	= 3 / 2	Г.	lz	= 0
384.Частица	находится в состоянии с волновой функцией

ψ ∼ Y ₅₄+2 Y ₅₃.Какие из нижеследующих величин имеют в этом

состоянии определенные значения?

А. проекция орбитального момента на ось z Б. проекция орбитального момента на ось y

В. проекция орбитального момента на ось x Г. квадрат орбитального момента

385. Частица находится в состоянии с волновой функцией ψ ∼ Y ₅₄+2 Y ₆₄.Какие из нижеследующих величин имеют в этом

состоянии определенные значения?

А. проекция орбитального момента на ось z Б. проекция орбитального момента на ось y

В. проекция орбитального момента на ось x Г. квадрат орбитального момента

386. Частица находится в состоянии,в котором ее момент имеетопределенное значение l = 3, а проекция с вероятностью 1/ 4 при-нимает значение m =1, а с вероятностью 3 / 4 – значение m = 2. Какой формулой может описываться волновая функция частицы?

А. ψ =

1 Y

−

3 i

Y

Б. ψ =

1 Y

− ^i ^3 Y

В. ψ =

i

Y

+

Y

Г. ψ =

^1 Y −

3 Y

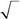
387. Какая функция получится в результате действия оператора^ˆ+

L

на функцию Y ₅₅ (ϑ, ϕ) (с точностью до множителя):

ˆ	(ϑ, ϕ) ∼ Y 56	(ϑ, ϕ)
А. L + Y 55
	ˆ
Б. функция L + Y 55 (ϑ, ϕ) тождественно равна нулю
ˆ	(ϑ, ϕ) ∼ Y 65	(ϑ, ϕ)
В. L + Y 55
ˆ	(ϑ, ϕ) ∼ Y 66	(ϑ, ϕ)
Г. L + Y 55

388. Какое из нижеследующих равенств является правильным(сточностью до множителя)?

ˆ	(ϑ, ϕ) ∼ Y 62 (ϑ, ϕ)	ˆ	(ϑ, ϕ) ≡ 0
А. L + Y 52	Б. L + Y 52
ˆ	(ϑ, ϕ) ∼ Y 53 (ϑ, ϕ)	ˆ	(ϑ, ϕ) ∼ Y 51(ϑ, ϕ)
В. L + Y 52	Г. L + Y 52

389. Какова«структура»сферических функций Y_lm (ϑ, ϕ)?А. некоторый многочлен от cos ϑ, умноженный на exp(imϕ) Б. некоторый многочлен от sin ϑ, умноженный на exp(imϕ)

В. некоторый многочлен от cos ϑ, умноженный на exp(imϕ) и

(для нечетных m) на sin ϑ

Г. некоторый многочлен от cos ϑ, умноженный на exp(imϕ) и

(для четных m) на sin ϑ.

390. Какой формулой определяется сферическая функция

Y ₁₂(ϑ, ϕ)?

А. cos ϑ e ^2 i ^ϕ	Б. cos ϑ e ^−^2 i ^ϕ	В. sin ϑ e ^2 i ^ϕ
Г. такой функции не существует

391. Какова «структура» сферических функций Y_lm (ϑ, ϕ)? А. некоторая функция от ϕ, умноженная на exp(imϑ) Б. некоторая функция от ϕ, умноженная на cos mϑ

В. некоторая функция от ϑ, умноженная на exp(imϕ) Г. некоторая функция от ϑ, умноженная на cos mϕ

392. От каких переменных зависит функция Y_{l 0}?

А. только от ϕ Б. только от ϑ В. только от r Г. от ϕ и от ϑ

393. Какая из нижеследующих функций не является сферической(сточностью до множителя)?

А.	f (ϑ, ϕ)=1	Б.	f (ϑ, ϕ)=cos ϑ
В.	f (ϑ, ϕ)=sin ϑe^i^ϕ	Г.	f (ϑ, ϕ)=cos ϑe ^− ^i^ϕ

394. Какая из нижеследующих функций является сферической(сточностью до множителя)?

А.	f (ϑ, ϕ)=sin ϑ sin ϕ	Б.	f (ϑ, ϕ)=cos ϑe ^− ^i^ϕ
В.	f (ϑ, ϕ)=sin ϑe^i^ϕ	Г.	f (ϑ, ϕ)=cos ϑe ^− ^i^ϕ
395.Частица находится в	состоянии с волновой функцией

sin ϑ sin ϕ. Какие значения орбитального момента и его проекции на ось z можно обнаружить при измерениях?

А. только l =1 и m =1

Б. только l =1, для проекции два значения m =1 и m = −1

В. для момента два значения l = 0 и l =1, для проекции – только m =1

Г. для момента два значения l = 0 и l =1 и для проекции два зна-чения m =1 и m = −1

396. Какие функции отcos ϑ входят в сферические функции?А. Γ -функция Б. присоединенные полиномы Лагерра

В. присоединенные полиномы Лежандра Г. присоединенные полиномы Эрмита

397. К каким функциям сводятся присоединенные полиномы Ле-жандра P_l ^{| m |} (x) при m = 0?

А. к полиномам Лежандра Б. к полиномам Лагерра В. к полиномам Эрмита

Г. ни к каким с самостоятельным именем собственным 398. К каким функциям сводятся присоединенные полиномы Ле-жандра P_l ^{| m |} (x) при m =1?

А. к полиномам Лежандра Б. к полиномам Лагерра В. к полиномам Эрмита

Г. ни к каким с самостоятельным именем собственным 399. Входящие в сферические функции присоединенные полиномы

Лежандра P_l ^{| m |} являются

А. некоторыми многочленами от ϑ Б. некоторыми многочленами от cos ϑ

В. некоторыми многочленами от cos ϑ для четных проекций m, и некоторыми многочленами от cos ϑ, умноженными на sin ϑ, для нечетных проекций m

Г. некоторыми многочленами от cos ϑ для четных моментов l, и некоторыми многочленами от cos ϑ, умноженными на sin ϑ, для нечетных моментов l

400. Частица находится в состоянии с волновой функциейcos² ϕ.

Измеряют проекцию момента на ось z. Какие значения проекции орбитального момента на ось z могут быть получены при измере-ниях в этом состоянии и с какими вероятностями?

А. 1, 2 и 3 с вероятностями ¼, ¼ и ½ Б. 1, 0 и −1 с вероятностями ¼, ½ и ¼ В. 0, 1 и 2 с вероятностями 1/3

Г. −2, 0, 2 с вероятностями 1/6, 2/3 и 1/6 401. Какая формула описывает условие ортогональности сфериче-ских функций?

π 2 π

А. _∫ d ϑ _∫ d ϕ sin ϕ Y_lm ^* (ϑ, ϕ) Y_λμ (ϑ, ϕ) = δ _{l λ} δ_mμ

π	2 π

Б. _∫ d ϑ sin ϑ _∫ d ϕ Y_lm ^* (ϑ, ϕ) Y_λμ (ϑ, ϕ) = δ _{l λ} δ_mμ

π	2 π

В. _∫ d ϑ _∫ d ϕ cos ϕ Y_lm ^* (ϑ, ϕ) Y_λμ (ϑ, ϕ) = δ _{l λ} δ_mμ

π	2 π

Г. ∫ d ϑ cos ϑ ∫ d ϕ Y ^* lm (ϑ, ϕ) Y_λμ (ϑ, ϕ) = δ _{l λ} δ_mμ

0 0

402. Какой формулой определяется условие ортогональности поли-номов Лежандра?

А. ^+∫^1 Pn (x) Pm (x) x ^2 dx ∼ δnm	Б. ^+∫^1 Pn (x) Pm (x) dx ∼ δnm
−1		−1
В. ^+∫^1	Pn (x) Pm (x) x ^3 dx ∼ δnm	Г. ^+∫^1	Pn (x) Pm (x) xdx ∼ δnm
−1		−1
(δnm – дельта-символ Кронекера)
403.	Какие значения может принимать индекс l в сферической

функции Y_{l 5} (ϑ, ϕ)? А. только l = 5

Б. целые значения в интервале −5 ≤ l ≤ 5 В. целые значения в интервале 0 ≤ l ≤ 5 Г. целые значения в интервале 5 ≤ l

404. Какие значения может принимать индекс m в сферической функции Y _{5 m} (ϑ, ϕ)?

А. только m = 5

Б. целые значения в интервале −5 ≤ m ≤ 5 В. целые значения в интервале 0 ≤ m ≤ 5 Г. целые значения в интервале 5 ≤ m

405. Какой формулой определяется условие ортогональности при-соединенных полиномов Лежандра?

А. ^+∫^1 Pl 1 ^| m | (x) Pl 2 ^| ^m ^| (x) dx ∼ δl 1 l 2	Б. ^+∫^1 Pl ^| m^1 ^| (x) Pl ^| ^m ^2 ^| (x) dx ∼ δm 1 m 2
−1				−1
В. ^+∫^1	^Pl 1	^| m^1 ^| (x) Pl 2	^| ^m ^2 ^| (x) dx ∼ δ l 1 l 2 δm 1 m 2	Г. никакой из них
−1
(δnm – дельта-символ Кронекера)	ˆ ^2	ˆ
					на сфе-
406.Каким будет результат действия оператора Lx	+ Ly

рическую функцию Y_lm (ϑ, ϕ)?

А.	^2 (l (l + 1) − m ^2) Ylm (ϑ, ϕ)	Б.	^2 (l (l + 1) − m ^2) Ylm +1 (ϑ, ϕ)
В.	^2 (l ^2 − m ^2) Ylm (ϑ, ϕ)	Г.	^2 (l ^2 − m (m +1)) Ylm +1 (ϑ, ϕ)

407. Какое утверждение относительно четности сферическихфункций Y_lm (ϑ, ϕ) является справедливым?

А. эти функции не обладают определенной четностью ни при каких l и m

Б. эти функции – четные для четных l и нечетные для нечетных l независимо от m

В. эти функции – четные для четных m и нечетные для нечетных m независимо от l

Г. эта функции – четные для четных l + m и нечетные для нечет-

ных l + m
408.Какое	утверждение относительно	четности функции
Y 81(ϑ, ϕ)+ Y 82(ϑ, ϕ)является справедливым?
А. четная	Б. нечетная	В.	неопределенной
четности	Г. четность приведенной функции зависит
от оператора четности
409.Что можно сказать о четности функции Y 72(ϑ, ϕ)+ Y 82(ϑ, ϕ)?
А. четная	Б. нечетная	В.	неопределенной
четности	Г. четность приведенной	функции зависит

от оператора четности

ГЛАВА 4. ТРЕХМЕРНОЕ ДВИЖЕНИЕ

Дата добавления: 2014-12-24