
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сферический осциллятор, кулоновский потенциал и бесконечно глубокая сферическая потенциальная яма 2 страница
|
|
|
|
508. Чему равна энергия второго стационарного p -состояния час-
| тицы массой | μ в сферической бесконечно глубокой прямоуголь- | |||||
| ной потенциальной яме радиуса a? | ||||||
| А. | 12 π 2 2 | Б. | 9 π 2 2 | В. | 16 π 2 2 | |
| 2 μa 2 | 2 μa 2 | 2 μa 2 | ||||
Г. аналитическое выражение для энергий p -состояния частицы в
сферической яме получить не удается 509. Частица в сферической бесконечно глубокой прямоугольной
потенциальной яме находится в состоянии с квантовыми числами nr =2, l =3, m =−2.Какова кратность вырождения этого уровня
энергии?
А. 5 Б. 7 В. 9 Г. 11
510. Волновая функция частицы в бесконечно глубокой сфериче-ской прямоугольной потенциальной яме представляет собой ли-нейную комбинацию собственных функций с квантовыми числами
nr =3, l =0, m =0и nr =2, l =1, m =0.Будет ли это состояниестационарным?
А. да Б. нет В. зависит от размера ямы Г. в некоторых случаях будет, в некоторых – нет
ГЛАВА 5. СПИН
511. Спин электрона равен1
А. s = −1/ 2
| Б. | s =1/ 2 | ||
| В. | s =1/ 2и s = −1/ 2с равными вероятностями | ||
| Г. | s =1/ 2и s = −1/ 2,вероятности зависят от состояния | ||
| 512.Проекция спина электрона на ось z равна | |||
| А. | sz | =1/ 2 | |
| Б. | sz | = −1/ 2 | |
| В. | sz | =1/ 2 и sz | = −1/ 2 с равными вероятностями |
| Г. | sz | =1/ 2 и sz | = −1/ 2, вероятности зависят от состояния |
513. Спин частицы равен3/4.Какие значения может приниматьпроекция ее спина на ось z?
| А. +3/4 и –3/4 | Б. +3/4, 3/2, -3/2 и –3/4 | |
| В. 3/2 и –3/2 | Г. спин таким быть не может | |
| 514.Спин частицы равен | s =5 / 2.Какова вероятность того,что | |
| проекция спина на ось z принимает значение sz = +5 / 2? | ||
| А. 1 | Б. 0 | В. ½ |
| Г. это зависит от состояния |
515. Спин частицы равен s =99 / 2.Какова размерность линейногопространства спиновых функций частицы?
А. 97 Б. 98 В. 99 Г. 100
516. Частица имеет спин s. В каких пределах меняется координата sz в списке аргументов этой функции ψ (r, sz)?
А. может быть любым числом от 0 до 1 Б. может быть любым числом от − s до s
В. может быть любым числом от − s до s через единицу Г. может быть любым целым числом от − s до s
517. В результате многократных измерений,выполненных над ан-самблем тождественных квантовых систем, были обнаружены сле-дующие вероятности различных проекций спина частицы на ось

1 Во всех задачах этой главы =1.
| y: w (sy = −1)=1/ 4, | w (sy =0)=1/ 4, | w (sy =1)=1/ 2.Чему ра- |
| вен спин частицы? | ||
| А. 1 | Б. 2 | В. 3 |
| Г. информации для ответа недостаточно | ||
| 518.Волновая функция частицы со спином s =1/ 2 ψ (r, sz)из- |
вестна. Вероятность того, что частица находится в малом элементе объема dV вблизи точки с радиусом-вектором r 0 равна
А. (| ψ (r 0, s z = − 1/ 2) |2 + | ψ (r 0, s z =1/ 2) |2) dV
| + s | | ψ (r, s | ) |2 ds | ||||||
| Б. | ∫ | z | dV | |||||
| z | ||||||||
| − s | ||||||||
| В. (| ψ (r 0, s z = −1) |2 + | ψ (r 0, s z = 0) |2 + | ψ (r 0, s z =1) |2) dV | ||||||||
| Г. | ψ (r, s | z | =1/ 2) |2 | dV | |||||
519. Волновая функция частицы со спином s =1/ 2 ψ (r, sz)из-
вестна. Каким из нижеперечисленных выражений определяется условие нормировки этой функции?
А. (| ψ (r, s z = − 1/ 2) |2 + | ψ (r, sz = 1/ 2) |2)=1
Б. ∫(| ψ (r, s z = − 1/ 2) |2 + | ψ (r, s z = + 1/ 2) |2) dV =1 (интегриро-
вание проводится по всем значениям координат)
| В. | +∞ | | ψ (r, s | ) |2 | ds | ||||
| ∫ | z | dV =1 (внутренний интеграл–по спино- | ||||||
| ∫ | z | |||||||
| −∞ |
вой переменной, внешний – по всем значениям координат)
| Г. dw (r) = | + s | | ψ (r, s | ) |2 | ds | по | ||||
| ∫ | z | dV (внутренний интеграл– | |||||||
| ∫ | z | ||||||||
| − s | |||||||||
| спиновой переменной, внешний – по всем значениям координат) | |||||||||
| 520.Волновая функция частицы со спином s =1/ 2 ψ (r, sz) | из- |
вестна. Какой смысл имеет величина ∫| ψ (r, s z =1/ 2) |2 dr (интег-
рирование проводится по всем значениям пространственных коор-динат)?
А. это вероятность того, что частица находится в малом элементе объема dr вблизи точки с радиусом-вектором r независимо от проекции спина Б. это вероятность того, что частица имеет проекцию спина
sz =1/ 2независимо от ее положения в пространстве
В. это вероятность того, что частица имеет проекцию спина sz = −1/ 2независимо от ее положения в пространстве
Г. это вероятность того, что частица находится в малом элементе объема dr вблизи точки с радиусом-вектором r с проекцией спи-на на ось z, равной sz =1/ 2
521. Спиновая волновая функция частицы равна
| −1/ 2 | |||||||
| ψ (s | ) = | . | |||||
| z | 3 / 2 | ||||||
| i | |||||||
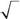 Чему равен спин такой частицы?
Чему равен спин такой частицы?
А. 1 Б. 3/2 В. 2 Г. 5/2
522. В каком из состояний,спиновые волновые функции которыхприведены ниже, частица имеет определенный спин?
| −1 | ||||||||
| А. только в состоянии | Б. только в состоянии | |||||||
| i | 0 | |||||||
| В. только в состоянии | Г. во всех перечисленных | |||||||
| −1 |
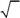
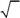 523. Какие из нижеперечисленных функций являются собственны-ми функциями оператора s ˆ2?
523. Какие из нижеперечисленных функций являются собственны-ми функциями оператора s ˆ2?
| А. только | и | Б. только | и | ||||
| 1 | 1 | − 1 | |||||
| Г. все двухкомпонентные столбцы | |||||||
| В. только | и | ||||||
| i | − i |
524. В каком из перечисленных состояний частица имеет опреде-ленную проекцию спина на ось z?
| А. ψ (sz) = | Б. ψ (sz) = | |||||||||
| 1 | ||||||||||
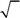 В. ψ (sz) = В. ψ (sz) =
| i | Г. во всех | ||||||||
| i | ||||||||||
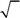 525. Какая из перечисленных функций является собственной функ-
525. Какая из перечисленных функций является собственной функ-
| цией оператора s ˆ z? | ||||||||||||
| А. ψ (sz) = | Б. ψ (sz) = | |||||||||||
| 0 | 1 | |||||||||||
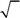 В. ψ (sz) = В. ψ (sz) =
| i | Г. никакая из перечисленных | ||||||||||
| i | ||||||||||||
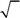
| / 2 | |||||||||||
| 526.Частица находится в состоянии ψ (sz)= | 1/ | . Что можно | ||||||||||
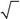 сказать о проекции спина на ось z в этом состоянии?
сказать о проекции спина на ось z в этом состоянии?
А. может принимать два значения sz = 3 / 2 и sz =1/ 2 с одина-ковыми вероятностями
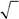
Б. может принимать два значения sz =1/ 2 и sz = −1/ 2 с вероят-
ностями 3 / 4 и 1/ 4 В. проекция спина частицы, волновая функция которой – двухком-
понентный столбец, равна 1/ 2 независимо от того, какие числа в этом столбце
Г. может принимать два значения sz =1/ 2 и sz = −1/ 2 с одинако-выми вероятностями
527. В каком из четырех состояний,спиновые волновые функциикоторых приведены ниже, частица имеет определенную проекцию спина на ось z?
| −1/ 2 | − i / 3 | ||||||||||||||||||
| А. ψ (s z)= 0 | Б. ψ (s z)= | ||||||||||||||||||
| i / 3 | |||||||||||||||||||
| −1/ 2 | |||||||||||||||||||
| 1/ 3 | |||||||||||||||||||
| 1/ | |||||||||||||||||||
| В. ψ (s | )= i | Г. ψ (s | )= | ||||||||||||||||
| z | z | 1/ 3 | |||||||||||||||||
| 0 | 1/ | ||||||||||||||||||
| z | |||||||||||||||||||
| 528.Чему равно среднее значение проекции спина на ось | в со- | ||||||||||||||||||
| стоянии ψ | (sz) = | ||||||||||||||||||
| ? | |||||||||||||||||||
| А. | Б. | ||||||||||||||||||
| В. | Г. | z | |||||||||||||||||
| 529.Чему равно среднее значение проекции спина на ось | в со- | ||||||||||||||||||
| стоянии ψ | (sz) = | − i / 2 | |||||||||||||||||
| ? | |||||||||||||||||||
| 3 / 2 | |||||||||||||||||||
| А. | Б. | ||||||||||||||||||
| В. | Г. | ||||||||||||||||||
| 1/ 2 | |||||||||||||||||||
| 530.Какая из четырех функций ортогональна функции | ? | ||||||||||||||||||
| i | 3 / 2 | ||||||||||||||||||
| −1/ 2 | 3 / 2 | i 3 / 2 | |||||||||||||||||
| А. | Б. | −1/ 2 | В. | −1/ 2 | |||||||||||||||
| i 3 / 2 | |||||||||||||||||||
| i | 3 / 2 | ||||||||||||||||||
| Г. | 1/ 2 | ||||||||||||||||||
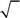
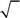
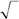
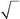
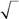
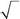
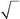

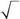
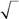
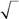
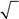
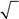
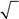 531. Чему равно скалярное произведение двух спиновых функций
531. Чему равно скалярное произведение двух спиновых функций
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 817; Нарушение авторских прав?; Мы поможем в написании вашей работы!