
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 4.8. Теорема об изменении кинетического момента относительно неподвижной оси
|
|
|
|
Пример 4.7
Теорема об изменении кинетического момента относительно неподвижной оси
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4
Маховик вращается вокруг оси, проходящей через его центр масс, с угловой скоростью 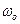 . Электрический тормоз создает тормозящий момент, пропорциональный угловой скорости маховика
. Электрический тормоз создает тормозящий момент, пропорциональный угловой скорости маховика  . Момент
. Момент 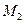 от трения в подшипниках считается постоянным (Рис.4.7). Определить, через какой промежуток времени
от трения в подшипниках считается постоянным (Рис.4.7). Определить, через какой промежуток времени 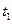 остановится маховик, если момент инерции маховика относительно оси вращения
остановится маховик, если момент инерции маховика относительно оси вращения  .
.
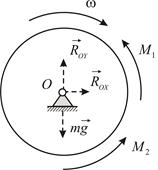
|
| Рис.4.7 |
Дифференциальное уравнение вращательного движения в рассматриваемом случае имеет вид:
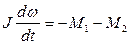 или
или 
Интегрируя полученное уравнение при заданных начальных условиях:
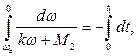
определяем время торможения:
 .
.
Шарик 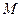 , находящийся в сосуде с жидкостью и прикрепленный к концу стержня
, находящийся в сосуде с жидкостью и прикрепленный к концу стержня  длины
длины 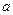 , приводится во вращение вокруг вертикальной оси
, приводится во вращение вокруг вертикальной оси 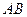 с начальной
с начальной
угловой скоростью 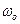 (Рис. 4.8). Сила сопротивления жидкости пропорциональна угловой скорости
(Рис. 4.8). Сила сопротивления жидкости пропорциональна угловой скорости  . Определить, через какой промежуток времени
. Определить, через какой промежуток времени 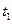 угловая скорость стержня станет в два раза меньше начальной, а также число оборотов
угловая скорость стержня станет в два раза меньше начальной, а также число оборотов 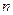 , которое сделает стержень за этот промежуток времени. Массу шарика считать сосредоточенной в его центре, массой стержня пренебречь.
, которое сделает стержень за этот промежуток времени. Массу шарика считать сосредоточенной в его центре, массой стержня пренебречь.
В динамике, также как и в статике, существенное значение имеет правильный выбор тела, движение которого будет рассматриваться. В данной задаче имеет смысл рассмотреть движение системы, состоящей из шарика и стержней 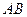 и
и  . При таком выборе неизвестные реакции опор не войдут в уравнение движения. На Рис. 4.8 изображены все внешние силы, действующие на указанную систему. Из всех этих сил только одна – сила сопротивления создает момент относительно оси вращения системы:
. При таком выборе неизвестные реакции опор не войдут в уравнение движения. На Рис. 4.8 изображены все внешние силы, действующие на указанную систему. Из всех этих сил только одна – сила сопротивления создает момент относительно оси вращения системы:
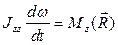 или
или 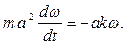
Поскольку формулировка задачи содержит несколько вопросов, имеет смысл интегрировать уравнение с переменным верхним пределом:
 откуда
откуда  и
и 
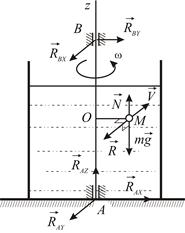
|
| Рис.4.8 |
Полагая в полученном решении  , определяем промежуток времени
, определяем промежуток времени 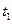 , по истечение которого угловая скорость уменьшится наполовину:
, по истечение которого угловая скорость уменьшится наполовину:

Число оборотов 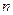 , сделанных стержнем за время
, сделанных стержнем за время 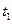 , связано с углом поворота стержня:
, связано с углом поворота стержня:  . Интегрируя равенство
. Интегрируя равенство 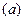 , получаем:
, получаем:

Подставляя сюда значение 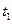 , получаем:
, получаем:
 и, следовательно,
и, следовательно, 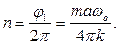
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 452; Нарушение авторских прав?; Мы поможем в написании вашей работы!