Пример 4.12

Плоскопараллельное движение твёрдого тела

Дифференциальные уравнения движения имеют вид:

;

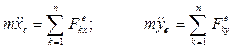где 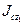— момент инерции тела относительно оси .

Однородный сплошной круглый диск катится без скольжения по наклонной плоскости, расположенной под углом 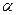к горизонту (Рис. 4.12). Определить диапазон углов наклона плоскости к горизонту, при которых возможно качение без скольжения, и скорость оси диска. В начальный момент диск находился в покое.

При изучении движения тела по наклонной плоскости имеет смысл одну из координатных осей направить вдоль наклонной плоскости, а вторую перпендикулярно к ней. Кинематическая и силовая схемы представлены на Рис. 4.12. Движение диска плоскопараллельное; скорость 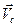центра масс параллельна наклонной плоскости. Дифференциальные уравнения плоскопараллельного движения принимают вид:

()

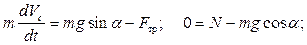
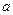где 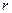– радиус диска; .

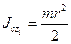Нетрудно видеть, что три уравнения движения содержат четыре неизвестные. По условию колесо катится без скольжения и, следовательно, точка касания – точка 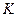является мгновенным центром скоростей. В таком случае скорость точки и угловая скорость колеса связаны равенством

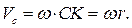
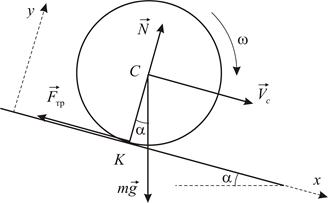
Рис. 4.12

Разрешим систему уравнений () относительно ускорения центра масс:

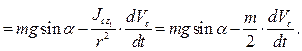
Отсюда:

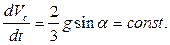
Тогда

Остается определить, при каких углах 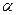возможно качение без скольжения. При отсутствии скольжения возникающая сила трения должна удовлетворять неравенству

()

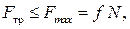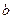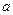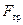где – коэффициент трения. Определяя из уравнений движения () и 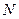, находим:

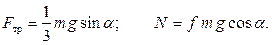
Тогда неравенство () представляется в виде:

Отсюда:

Дата добавления: 2014-12-25