Пример 4.15

Примеры динамического исследования сложных систем

При изучении движения механической системы, как правило, необходимо использовать несколько теорем. Если система состоит из нескольких твердых тел, то в большинстве случаев оказывается удобным (а иногда необходимым) разделить систему на части, рассматривая движение каждого тела, входящего в систему, в отдельности.

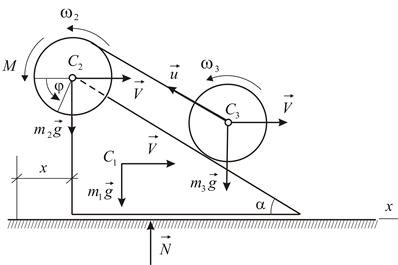
Призма (тело 1) массы 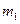может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки (тело 2). Конец троса прикреплен к оси катка (тело 3), который катится без проскальзывания по боковой поверхности призмы (Рис. 4.15). Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы 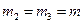и одинакового радиуса 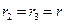. К барабану лебедки приложен постоянный вращающий момент 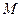. Определить движение системы, если в начальный момент времени она находилась в покое.

Система имеет две степени свободы. В качестве параметров, определяющих положение системы примем координату 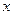призмы и угол поворота 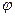барабана лебедки.

Рис. 4.15

Заметим, что внешние силы, приложенные к системе в целом, не имеют проекций на направление движения призмы (Рис. 4.15). Записывая теорему об изменении количества движения механической системы в проекциях на координатную ось ,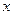

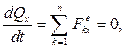
получаем:

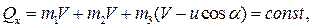
где 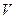– скорость призмы, а 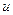– относительная скорость оси катка. Учитывая, что в начальный момент система находилась в покое, получаем:

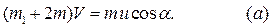
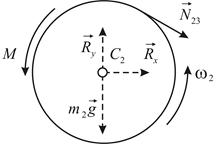
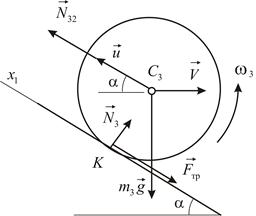
Рис. 4.16		Рис. 4.17

Дифференциальное уравнение вращательного движения для барабана лебедки имеет вид (Рис. 4.16):

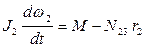
или, учитывая, что 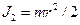и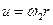

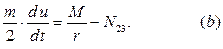
Для катка запишем теорему о движении центра масс в проекциях на направление оси 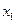(вдоль наклонной плоскости) и дифференциальное уравнение вращения (Рис. 4.17):

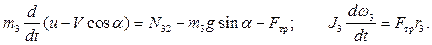
Точка 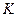является мгновенным центром скоростей катка в его относительном движении. Учитывая, что и 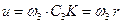, получаем:

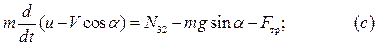
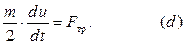
Исключая из системы уравнений 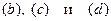, силы 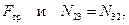получаем:

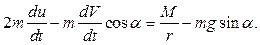
Это уравнение после интегрирования при нулевых начальных условиях принимает вид:

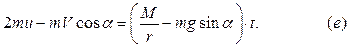
Задача свелась к решению системы уравнени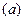й и 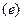. Получаем:

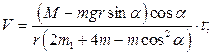
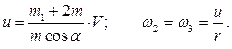
Пример 4.16

Каток массы 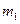радиуса 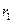катится без скольжения по горизонтальной поверхности под действием приложенного к нему постоянного вращающего момента 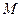. Трос, намотанный на боковую поверхность катка, сходит с него горизонтально и попадает на неподвижный блок массы 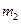и радиуса 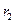(Рис.4.18). К свободному концу троса привязан груз массы 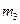. Считая каток и блок сплошными однородными цилиндрами определить скорость оси катка 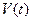. если в начальный момент времени система находилась в покое.

Рассматривая движение каждого из тел системы в отдельности, записываем: теорему о движении центра масс катка в проекциях на горизонтальное направление:

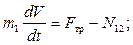
дифференциальное уравнение вращательного движения катка:

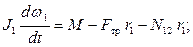
дифференциальное уравнение вращательного движения блока:

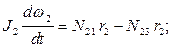
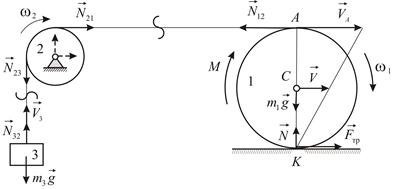
Рис. 4.18

и теорему о движении центра масс груза в проекциях на вертикальное направление:

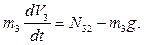
Учитывая очевидные кинематические соотношения:

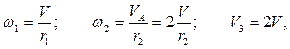
а также тот факт, что

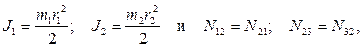
получаем дифференциальное уравнение:

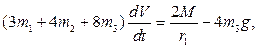
интегрируя которое при нулевых начальных условиях, находим:

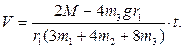
Дата добавления: 2014-12-25