Пример 5.4

Пример 5.3

Шарик 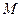массы 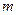привязан к концу нерастяжимой нити длины 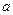, другой конец которой закреплен. Нить отклонили от вертикали на угол 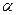и отпустили шарик без начальной скорости (Рис. 5.4). Определить скорость шарика при прохождении им нижней точки траектории, а также натяжение нити в этом положении.

Для решения задачи используем дифференциальное уравнение движения точки в проекциях на главную нормаль к траектории (1.4):

которое в нижней точке траектории принимает вид

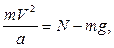
и теорему об изменении кинетической энергии:

Рис. 5.4

или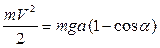

поскольку в рассматриваемом случае начальная кинетическая энергия равна нулю, а работу совершает только сила тяжести

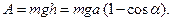
Таким образом,

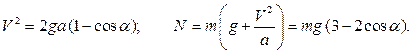
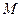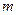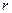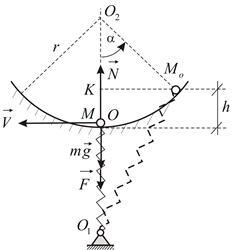
Тело , масса которого равна , скользит по гладкой цилиндрической поверхности радиуса . К телу прикреплена пружина жесткости , второй конец которой прикреплен к шарниру . Длина недеформированной пружины, массой которой можно пренебречь по сравнению с массой тела, равна . Расстояние от шарнира до цилиндрической поверхности (Рис. 5.5). Определить скорость тела и его давление на цилиндрическую поверхность в момент прохождения положения статического равновесия, если в начальный момент времени тело смещено от положения равновесия 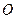по дуге окружности на центральный угол 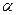и отпущено без начальной скорости.

На тело действуют две потенциальные силы – сила реакции пружины 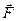и сила тяжести , а также реакция гладкой поверхности, работа которой равна нулю. Следовательно, имеет место закон сохранения полной механической энергии.

В начальном положении имеем

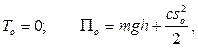
где – начальное удлинение пружины, 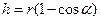– высота точки над нулевым уровнем, проходящим через точку 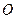. Из прямоугольного треугольника получаем:

.

Рис. 5.5

Отсюда:

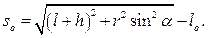
В момент прохождения телом положения статического равновесия имеем:

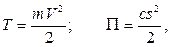где

Подставляя найденные величины в закон сохранения полной механической энергии

,

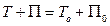получаем:

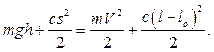
Отсюда:

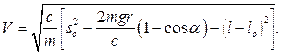
Для определения давления тела на опорную поверхность используем теорему о движении центра масс тела в проекциях на главную нормаль в нижней точке траектории:

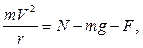
где – сила реакции пружины. Отсюда получаем давление тела на поверхность, равное по модулю реакции:

.

Дата добавления: 2014-12-25