Перша чудова границя

Чудові границі(перша і друга чудові границі).

.

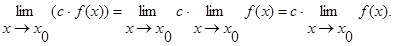
Теорема 17.9. Границя дробу рівна границі чисельника, діленій на границю знаменника, якщо границя знаменника не рівна нулю:

Розглянемо приклад.

Приклад 17.3. Обчислить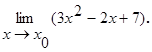

○

●

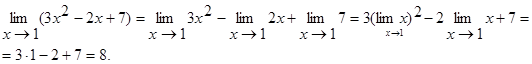Приклад 17.4. Обчислити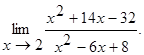

○ Тут застосувати теорему про границю дробу не можна, оскільки границя знаменника, при, рівний 0. Крім того, границя чисельника рівна 0. В таких випадках говорять, що маємо невизначеність вигляду 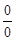. Для її розкриття розкладемо чисельник і знаменник дробу на множники, потім скоротимо дріб на (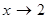, але ):

●

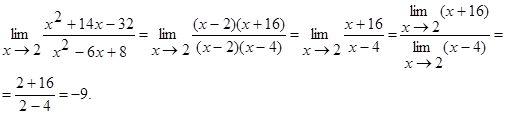Приклад 17.5. Обчислити

○ Тут ми маємо справу з невизначеністювигляду 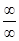. Для знаходження границі даного дробу розділимо чисельник і знаменник на :

.

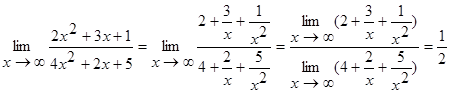Функція 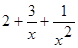є сума числа 2 і н.м.ф., тому

●

При обчисленні границь виразів, що містять тригонометричні функції, часто використовують границю

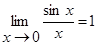(17.11)

званий першою чудовою границею. Читається: границя відношення синуса до його аргументу рівна одиниці, коли аргумент прямує до нуля. Доведемо рівність (17.11).

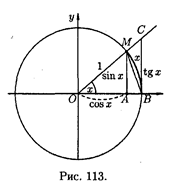Візьмемо коло радіусау 1, позначимо радіану міру кута МОВ через х (див. рис. 113).

Нехай на рис. |AM|=sinx, дуга МВ чисельно рівна центральному куту х |BC|=tgx. Очевидно, маємо 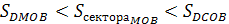. На підставі відповідних формул геометрії одержуємо. Розділимо нерівності на, отримаєм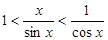о або . Оскільки 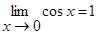і, то по ознаці (про границю проміжної функції) існування границь

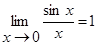. (17.12)

Нехай тепер 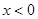. Маємо 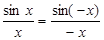, де . Тому

. (17.13)

З рівності (17.12) і (17.13) випливає рівність (17.11).

Приклад 17.6. Знайти

○ Маємо невизначеність вигляду 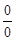. Теорема про границю дробу незастосовна. Позначимо 3x=t; тоді при 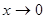і , тому

●

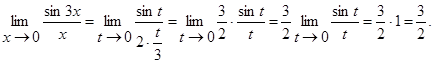Приклад 17.7. Знайти

○ ●

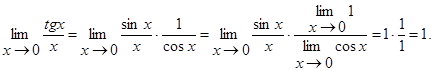Дата добавления: 2014-12-26