Дослідження функції за допомогою похідної. Зростання та спадання функції

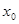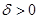Функція називається зростаючою в точці , якщо існує інтервал , де , який знаходиться в проміжку 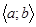, і такий, що для всіх з інтервалу 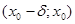і 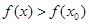для всіх з інтервалу .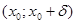

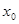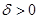Функція називається спадною в точці , якщо існує інтервал , де , який знаходиться в проміжку 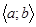, і такий, що 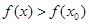для всіх з інтервалу 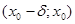і для всіх з інтервалу .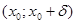

Означення. Функція y = f (x) має мінімум (максимум) у точці x ₀, якщо існує такий окіл точки x₀, що для всіх точок x ¹ x ₀ цього околу виконується нерівність f (x ₀)< f (x) (f (x ₀)< f (x)).

y

x ₀ x

Рис. 5.1.

Функція, показана на рис. 5.1, має два мінімуми та три максимуми. Нагадаємо, що поняття мінімуму та максимуму об’єднані в термін “екстремум”.

Теорема (необхідна умова існування екстремуму). Якщо диференційовна функція f (x) в точці x ₀ має екстремум, то в цій точці похідна f ¢(x ₀) =0.

Теорема. Якщо на деякому відрізку [ a; b ] похідна f ¢(x) від деякої функції є додатною (від’ємною), то на цьому відрізку функція f (x) зростає (спадає)

Теорема (перша достатня умова існування екстремуму). Якщо похідна f ¢(x) від деякої диференційоної функції f (x) в точці x = x ₀ дорівнює нулю і при x < x ₀ похідна f ¢(x)>0, а при x > x ₀ похідна f ¢(x)<0, то точка x ₀ є точкою максимуму. Якщо ж похідна f ¢(x) в деякому околі точки x ₀ змінює знак з від’ємного на додатний, то точка x ₀ є точкою мінімуму.

Теорема (друга достатня умова існування екстремуму). Якщо в точці x ₀ диференційовної функції y = f (x) перша похідна f ¢(x)=0, а друга f ¢¢(x)<0, то в цій точці є максимум (мінімум, якщо f ¢¢(x)>0).

Поняття мінімуму та максимуму не треба плутати з поняттями найбільшого та найменшого значень функції на деякому інтервалі.

Зазначимо, що умова f ¢(x)=0 не є достатньою для існування екстремуму функції y = f (x).

Нехай y = f(x) ‑ деяка функція та (x ₀; y ₀) ‑ точка з області визначення цієї функції. Проведемо через точку (x ₀; y ₀) дотичну до кривої (рис. 5.2).

y y = f (x)

D y

d y

d x =D x

a

x ₀ x

Рис. 5.2.

Рівняння цієї дотичної – це пряма

y = f (x ₀) + f ¢(x ₀)(x - x ₀) (5.2)

Величина f ¢(x ₀) = k = tga є нахилом кривої y = f (x) в точці x ₀.

Означення. Диференціалом від функції y = f (x) називається вираз dy = f ¢(x) dx, де dx = D x ‑ приріст аргументу (рис. 5.2).

Приклад. Нехай y = ln(x ²+1).

Тоді .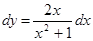

Приклад. Знайти екстремуми та інтервали зростання і спадання функції y = x ³ – 6 x ² +9 x.

Знаходимо похідну y ¢ =3 x ² – 12 x +9.

Розв’язуємо рівняння 3 x ² – 12 x +9=0, звідки x ₁=1; x ₂=3.

Досліджуємо знаки першої похідної

Інтервал	(-∞; 1)		(1; 3)		(3; +∞)
Знак f ¢(x)	+		-		+
Поведінка y = f (x)	Зростає	Максимум	Спадає	Мінімум	Зростає

Точки x ₁=1 та x ₂=3 можна також дослідити згідно з другою достатньою умовою екстремуму:

y ²(x) = 6 x – 12;

y ²(1) = - 6 < 0, отже, в точці x =1 функція y = x ³ – 6 x ² +9 x досягає максимуму;

y ²(3) = 6 > 0, отже, в точці x =3 ця функція має мінімум.

Означення. Функція f (x) називається випуклою (випуклою вверх) на відрізку [ a; b ], якщо на цьому інтервалі її графік розташований нижче від її дотичної (рис. 5.3,а). Функція f(x) називається увігнутою (випуклою вниз), якщо на [ a; b ] цей графік розташований нижче від дотичної (рис. 5.3,б).

Дата добавления: 2014-12-26