Асимптоти графіка функції. Вертикальна, горизонтальна та похила асимптоти

Нехай крива задана рівнянням 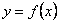, де 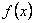є неперервною функцією на відрізку . Тоді задана крива всіма своїми точками знаходитиметься в замкненому прямокутнику , де є найбільше значення функції 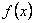на відрізку .

Якщо функція 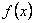задана на нескінченному проміжку або у випадку, коли проміжок скінчений, але містить точки розриву другого роду заданої функції, то криву не завжди можна розмістити в прямокутнику. Тоді крива або окремі її вітки йдуть в нескінченність. При цьому може трапитися так, що крива на нескінченності, “розпрямляючись”, наближається до деякої прямої лінії (рис.6.21).

Означення. Пряма лінія називається асимптотою кривої , якщо відстань точки кривої до прямої прямує до нуля, коли точка по кривій рухається в нескінченність, тобто

.

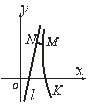
Рис.6.21

Асимптоти розрізняють трьох типів: “горизонтальні” (паралельні осі ); “вертикальні” (паралельні осі ) і - “похилі”.

Горизонтальні асимптоти мають рівняння , якщо 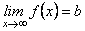; вертикальні рівняння , якщо .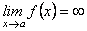

Для існування похилих асимптот необхідне існування (і скінченність) обох границь (6.108) і (6.109). При цьому можливі такі окремі випадки.

1. Обидві границі існують, скінченні і не залежать від знаку:

;

.

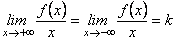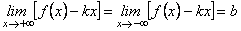В цьому випадку пряма буде двосторонньою асимптотою графіка.

2. Обидві границі існують і при , і при , але

.

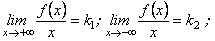
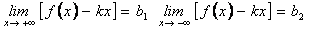41. Схема дослідження функції. Побудова графіка.

Наочне уявлення про хід зміни функції дає її графік, тому його побудова повинна бути заключним етапом дослідження функції, в якому мають використовуватися всі результати її дослідження. Для зручності дослідження функції рекомендуємо вести в деякій певній послідовності.

1. Знайти область існування функції. Це дає змогу визначити ті точки осі абсцис, над якими пройде чи не пройде графік функції.

2. Знайти точки перетину графіка з координатними осями. Для цього треба розв’язати дві системи рівнянь:

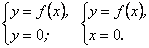
Перша система дає точки перетину з віссю , друга – з віссю .

3. Дослідити функцію на періодичність, парність і непарність. Розв’язання цього питання полегшить побудову графіка в тому розумінні, що її доведеться виконувати не в усій області існування функції, а тільки в її частині. Так, якщо 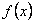- періодична функція з періодом , то графік достатньо побудувати на відрізку числової осі, довжина якого дорівнює , а потім цю частину графіка повторити на кожному відрізку довжини . Якщо функція парна, то графік функції симетричний відносно осі , якщо не тільки при , а потім симетрично відобразити і на від’ємні .

4. Знайти точки розриву функції та дослідити їх характер. Це допоможе встановити вигляд графіка функції поблизу цих точок.

5. Знайти значення функції на кінцях відрізків, де визначена функція. Якщо область існування функції є інтервал (півінтервал) або кілька інтервалів (півінтервалів), то треба знайти граничне значення функції, коли наближається до одного з кінців розглядуваних проміжків.

6. Визначити інтервали монотонності функції.

7. Знайти екстремальні точки і побудувати їх на площині.

8. Знайти інтервали вгнутості та опуклості кривої, яка є графіком функції.

9. Знайти точки перетину і побудувати їх на площині.

10. Знайти асимптоти графіка функції.

11. Побудувати графік функції.

Приклад. Дослідити функцію та побудувати її графік.

Р о з в ’ я з о к.

1. Оскільки задана функція дробово-раціональна, то вона не існує в точках, де знаменник дорівнює нулю:

,

звідки .

Отже, область існування є об’єднання множин .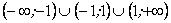

2. Нехай , тоді . Нехай , тоді . Отже, графік перетинає координатні осі в точці 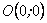, тобто графік проходить через початок координат.

3. Функція не періодична. Проте вона є непарною, тому розглядатимемо тільки .

4. Чисельником і знаменником є многочлени, неперервні на всій числовій осі. Тому точкою розриву при є тільки одна точка . Дослідимо її характер. Знайдемо односторонні границі

.

Отже, є точка розриву другого роду; пряма є вертикальною асимптотою.

5. Досліджуємо функцію на кінцях проміжків, вона визначена. В точці ми її дослідили, тепер знайдемо

.

6. Обчислимо

.

Розв’яжемо нерівність :

.

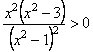Звідси, в інтервалі 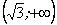функція зростає, а в інтервалах 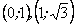- спадає.

7. Знайдемо екстремальні точки. Розв’яжемо рівняння :

,

звідки матимемо стаціонарні точки .

При переході через точку похідна знака не змінює, а при переході через точку - змінює знак “-” на “+”. Тому не є екстремальною точкою, а є точкою мінімуму:

.

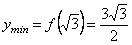8. Знаходимо інтервали вгнутості та опуклості графіка функції

.

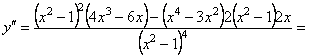
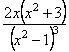Розв’яжемо нерівність :

.

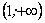Ця нерівність справджується при . Отже, в інтервалі крива вгнута, а в інтервалі - опукла.

9. Знаходимо точку перегину. Для цього розв’язуємо рівняння : 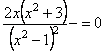, звідки .

При проходженні через точку похідна змінює знак “+” на “-”. Точка 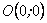є точка перегину.

10. Знаходимо похилі асимптоти:

;

.

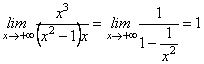Отже, .

Рівняння похилої асимптоти: .

11. Будуємо графік функції (рис.6.22).

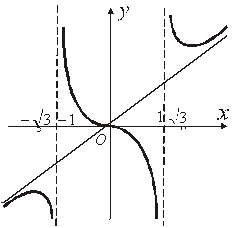
Рис.6.22

Дата добавления: 2014-12-26