
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические рекомендации. Вопросы, выносимые на обсуждение
|
|
|
|
Вопросы, выносимые на обсуждение
1. Составление уравнений касательной и нормали к плоской кривой.
2. Применение правил Лопиталя при вычислении пределов функции.
3. Разложение основных элементарных функций по формуле Тейлора.
Для подготовки к занятию дома
1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.
2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.
3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.
4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.
5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.
На занятии по указанию преподавателя
1. Обсудите вопросы из теоретических заданий для развития и контроля владения компетенциями.
2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.
Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.
Рекомендуемая литература
[1] глава 8 п. 8.6., п. 8.9.
[2] глава VII § 1.
[3] глава 6 § 25.
[4] часть II занятия 30, 36.
[5] глава 2 § 2.3.
[6] глава 6 §§ 1-3.
[7] глава VI §§ 1-3.
[8] глава 5 §§ 13-14.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
1. Составьте уравнения касательной и нормали к параболе  в точке
в точке 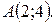
Решение. Так как надо составить уравнения касательной и нормали в точке 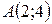 , то
, то 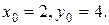
Тогда уравнение касательной в точке 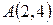 будет иметь вид:
будет иметь вид:  или
или 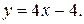
А уравнение нормали: 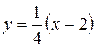 или
или 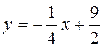 .
.
2. С помощью правила Лопиталя найдите пределы:
а) 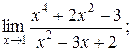 б)
б) 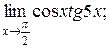 в)
в) 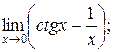 г)
г) 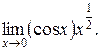
Решение. а) В данном пределе имеем неопределенность вида 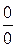 . По правилу Лопиталя заменим отношение этих величин отношением их производных:
. По правилу Лопиталя заменим отношение этих величин отношением их производных:
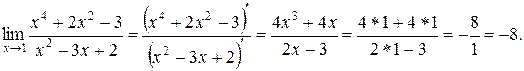
Замечание. Аналогично можно раскрыть неопределенность вида 
б) В данном пределе имеем неопределенность 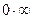 . Сведем эту неопределенность к виду
. Сведем эту неопределенность к виду 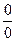 , а затем применим правило Лопиталя:
, а затем применим правило Лопиталя:
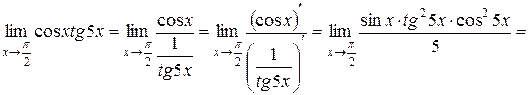
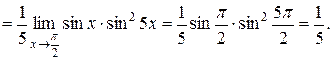
в) В данном пределе имеем неопределенность вида  Преобразуем функцию к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или к бесконечности, затем применим правило Лопиталя:
Преобразуем функцию к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или к бесконечности, затем применим правило Лопиталя:
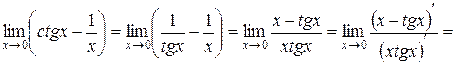
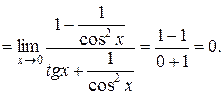
г) В данном пределе имеем неопределенность вида  . Заметим сразу, что таким образом можно раскрыть неопределенности вида
. Заметим сразу, что таким образом можно раскрыть неопределенности вида  и
и  . Эти случаи нахождения предела функции сводятся к случаю
. Эти случаи нахождения предела функции сводятся к случаю  (а затем к случаю
(а затем к случаю 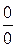 и
и  ) следующим путем: функция логарифмируется и сначала находится предел ее логарифма, а затем по найденному пределу логарифма находится и предел самой функции. Таким образом, пусть
) следующим путем: функция логарифмируется и сначала находится предел ее логарифма, а затем по найденному пределу логарифма находится и предел самой функции. Таким образом, пусть 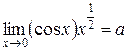 .
.
Логарифмируем функцию и находим предел ее логарифма:
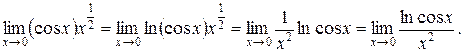
Здесь нахождение предела свелось к случаю 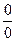 . Применяя правило Лопиталя, получим:
. Применяя правило Лопиталя, получим: 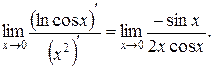 Неопределенность
Неопределенность 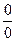 осталась. Применим правило Лопиталя 2-й раз:
осталась. Применим правило Лопиталя 2-й раз:
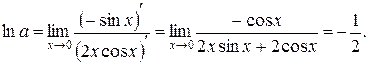
Теперь по найденному пределу логарифма функции находим искомый предел самой функции: 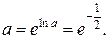
Таким образом: 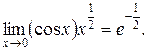
3. Разложите многочлен 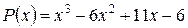 по степеням
по степеням  по формуле Тейлора.
по формуле Тейлора.
Решение. Найдем значение многочлена и его производных при 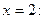
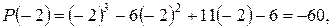
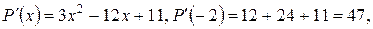
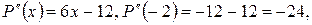
 и все последующие производные равны 0. Тогда для разложения многочлена по степеням
и все последующие производные равны 0. Тогда для разложения многочлена по степеням 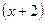 по формуле Тейлора имеем:
по формуле Тейлора имеем:
 т.е.
т.е.
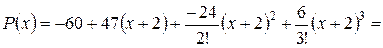
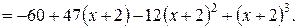
Теоретические задания
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 323; Нарушение авторских прав?; Мы поможем в написании вашей работы!