Теорема Безу

Многочлени від однієї змінної. Ділення многочленів з остачею.

Розділ 1. АЛГЕБРАЇЧНІ ПЕРЕТВОРЕННЯ

Загальний вигляд многочлена:

,

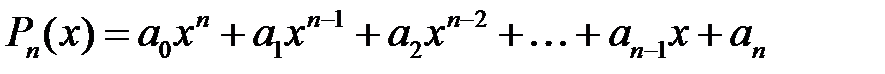де 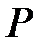– ім'я; 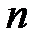– степінь; – аргумент; 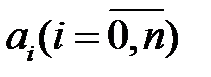– коефіцієнт; 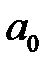– старший коефіцієнт (якщо 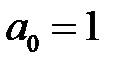– многочлен зведений); 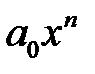– старший член; – вільний член.

Зв'язок між компонентами при діленні многочленів:

.

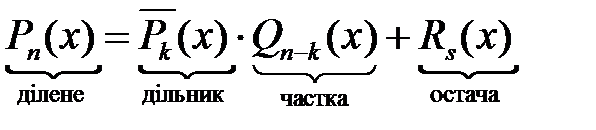Завжди 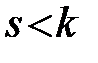; якщо 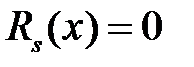, то многочлен 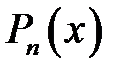ділиться на многочлен 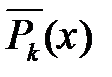(пишуть 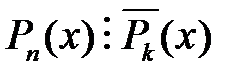). Зокрема, 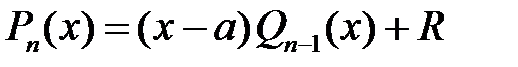, де 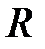– число; якщ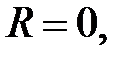о то .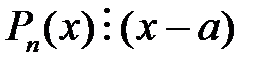

Теорема Безу. Остача від ділення многочле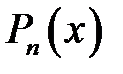на на 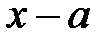дорівнює значенню многочлена при .

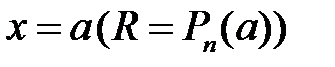Теорема (ознака подільності многочлена на 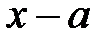). Для подільності многочле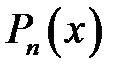на на 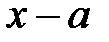необхідно і достатньо, щоб 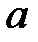було коренем многочлена 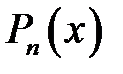, тобто .

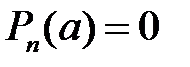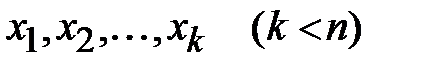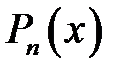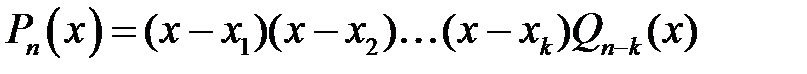Висновок. Якщо - корені многочлена , то , де 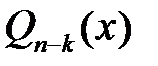– многочлен степеня 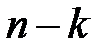; 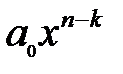– його старший член.

Приклад 1.1. Розділити многочлен на многочлен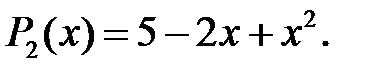

Розв’язання. Зобразимо ці многочлени в канонічних формах:

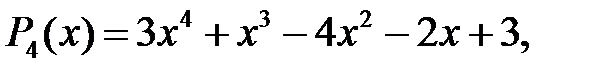
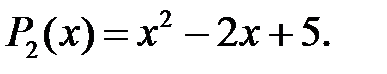
Виконаємо ділення стовпчиком:

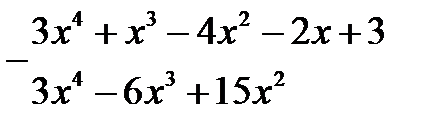
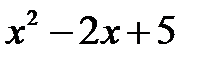
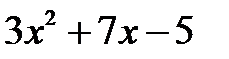
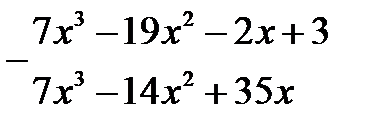
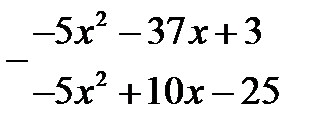
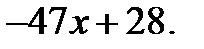
Частка – 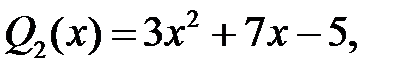остача –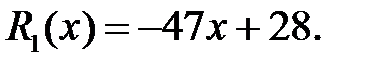

Зауваження. Справедливі рівності 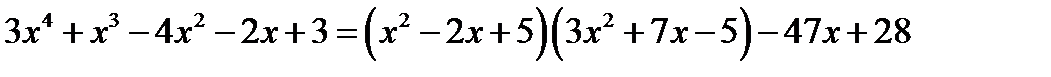, або

.

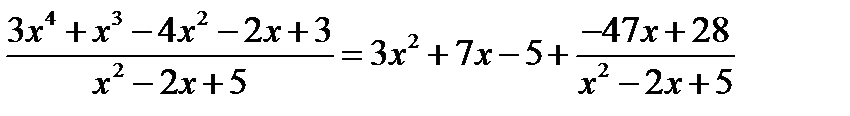Розглянемо ділення многочленів від декількох аргументів. Виберемо один із цих аргументів і умовно будемо вважати многочлени залежними тільки від цього аргументу, інші аргументи умовно о вважатимемо параметрами. Запишемо многочлени в канонічних формах і виконаємо ділення стовпчиком.

Приклад 1.2. Розділити 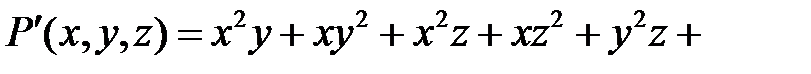многочлен

на многочлен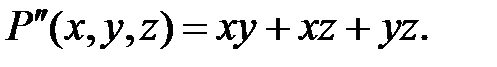

Розв’язання. Будемо вважати ці многочлени многочленами відносно аргументу 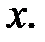Запишемо їх в канонічних формах:

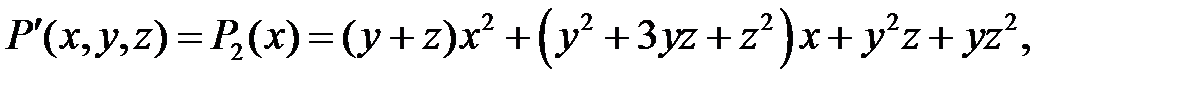
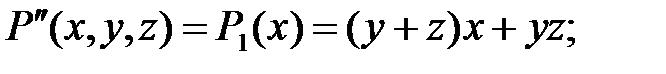
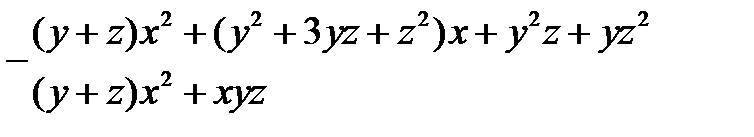
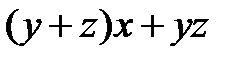
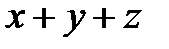
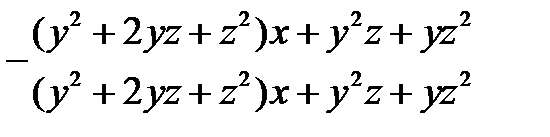
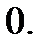
Частка – 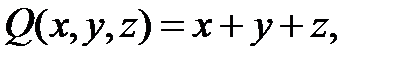остача –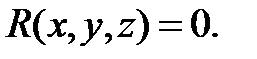

Розглянемо ділення многочлена на двочлен

Приклад 1.3. Знайти остачу від ділення многочле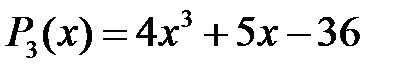на на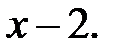

Розв’язання. За теоремою Безу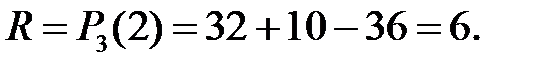

Приклад 1.4. Перевірити подільність многочле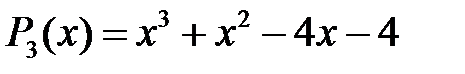на на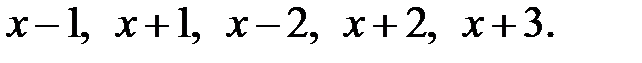

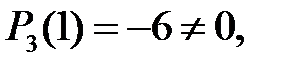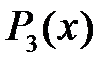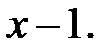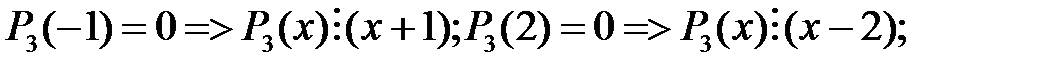
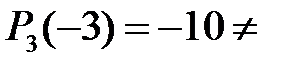
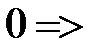
Розв’язання. Оскільки то не ділиться на Далі 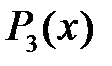не ділиться на .

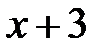Зауваження. Справедлива рівність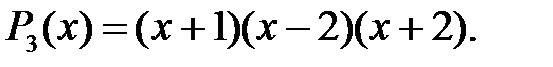

Дата добавления: 2014-12-26