
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні формули тригонометрії. Формули зведення. Перетворення тригонометричних виразів
|
|
|
|
Завдання для самостійної роботи
2.01.Побудувати кут: 1) синус якого дорівнює: a) 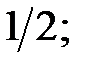 b)
b) 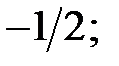 c)
c) 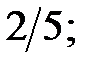 2) косинус якого дорівнює: a)
2) косинус якого дорівнює: a) 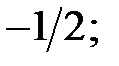 b)
b) 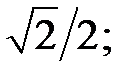 c)
c) 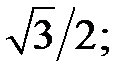 3) тангенс якого дорівнює: a)
3) тангенс якого дорівнює: a) 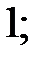 b)
b) 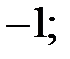 c)
c) 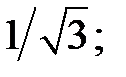 котангенс якого дорівнює: a)
котангенс якого дорівнює: a)  b)
b) 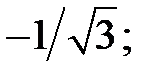 c)
c)  .
.
2.02. Визначити знаки таких виразів: а) 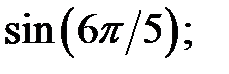 b)
b) 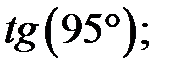 c)
c) 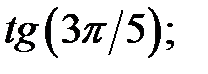
d) 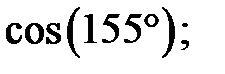 e)
e) 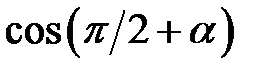 , де
, де 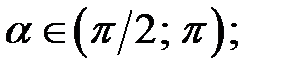 f)
f) 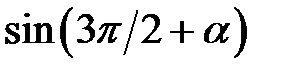 , де
, де 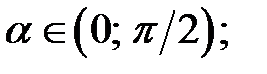
g) 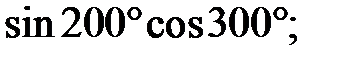 h)
h) 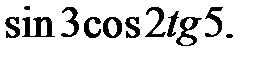
2.03.Обчислити: а) 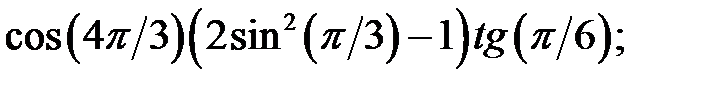 b)
b) 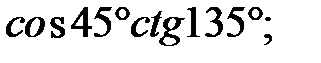
c)  d)
d) 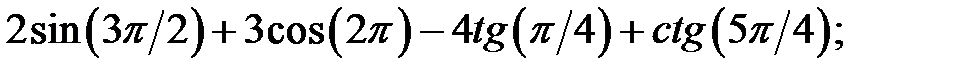
e) 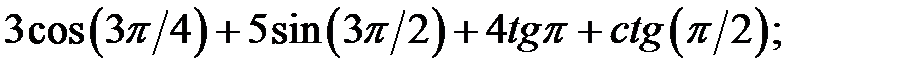 f)
f) 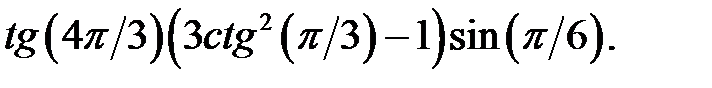
2.04. Для яких чвертей проміжку  виконуються нерівності: а)
виконуються нерівності: а) 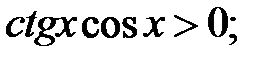
b)  c)
c) 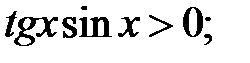 d)
d) 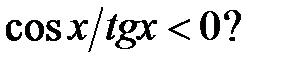
2.05. До яких чвертей належить кут, якщо: а) 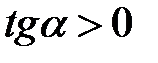 ; b)
; b) 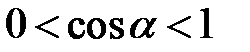 ; c)
; c) 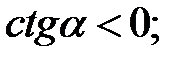
d) 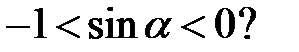
2.06. Чи існує таке значення 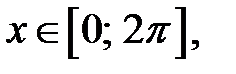 щоб: а)
щоб: а) 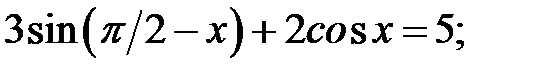
b) 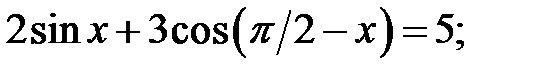 c)
c) 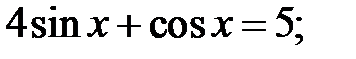 d)
d) 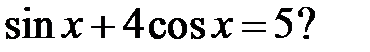
2.07. Обчислити 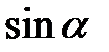 ,
, 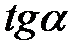 ,
, 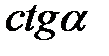 , якщо: а)
, якщо: а) 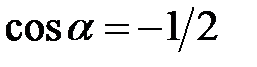 і
і 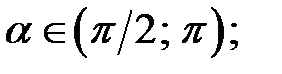 b)
b) 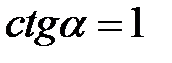 і
і 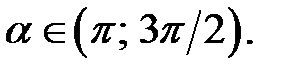
У процесі перетворення тригонометричних виразів широко застосовуються такі формули.
1. Формули додавання:
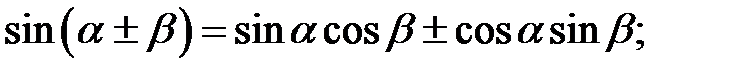

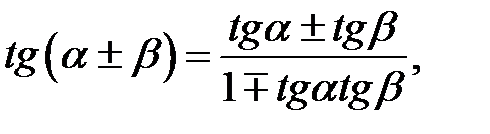
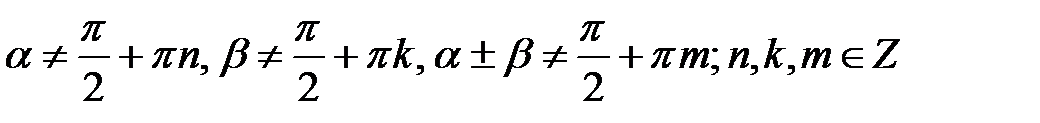 .
.
2. Формули кратних аргументів:
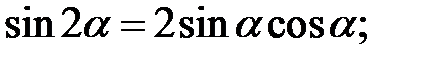
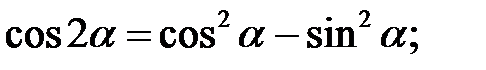
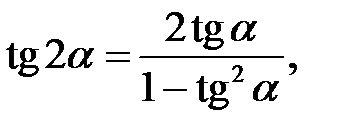
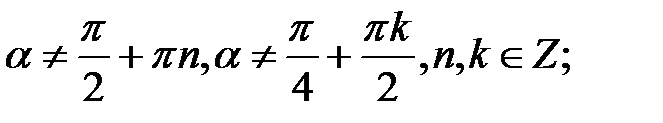
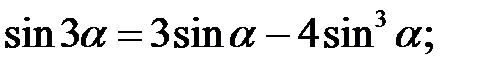
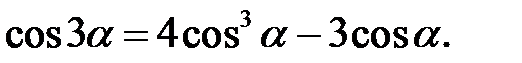
3. Формули половинного аргументу:
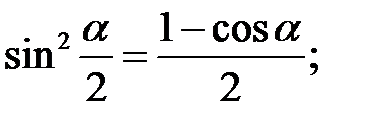
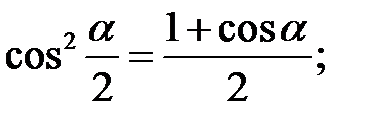
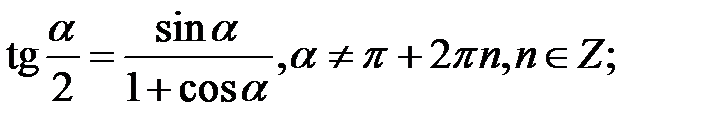
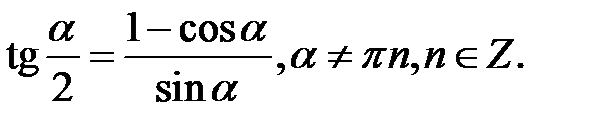
4. Формули перетворення суми і різниці в добуток:
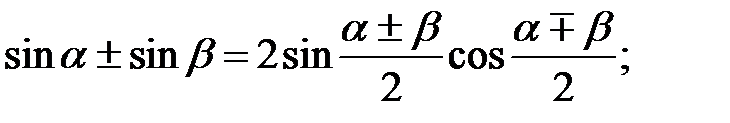
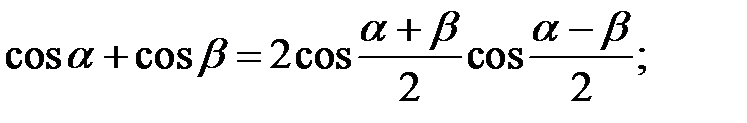
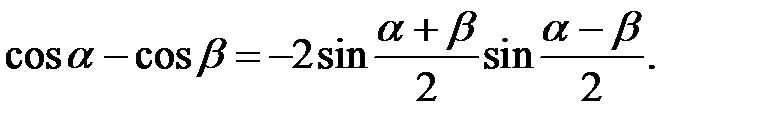
5. Формули перетворення добутку в суму і різницю:
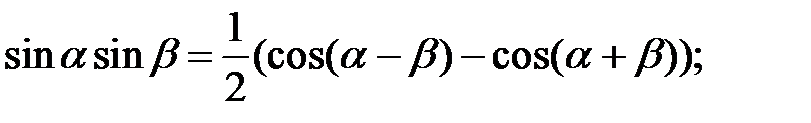
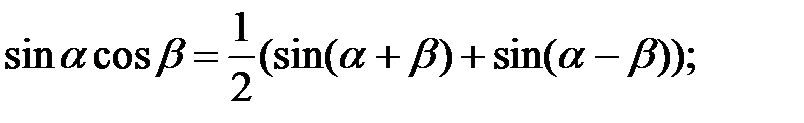
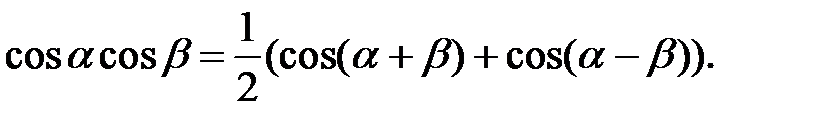
6. Співвідношення між 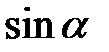 ,
, 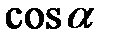 ,
, 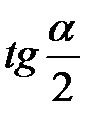 :
:
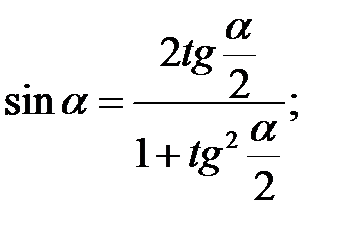
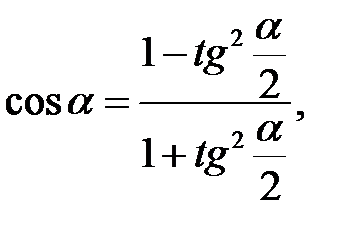
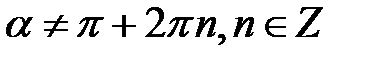 .
.
Також мають місце формули зведення. Формули зведення перетворюють тригонометричні функції від аргументів 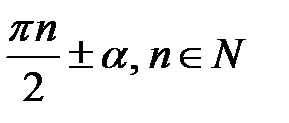 до функцій з аргументом
до функцій з аргументом  .
.
Для зручності у користуванні формулами зведення використовують такі правила:
а) кут  завжди вважається гострим;
завжди вважається гострим;
б) ціле число періодів завжди можна відкинути;
в) якщо кут 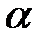 відкладається від горизонтального діаметра
відкладається від горизонтального діаметра 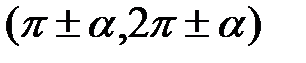 , то назва функції зберігається; якщо кут
, то назва функції зберігається; якщо кут 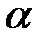 відкладається від вертикального діаметра
відкладається від вертикального діаметра 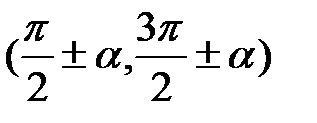 , то назва функції змінюється (синус – на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс).
, то назва функції змінюється (синус – на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс).
Приклад 2.4. Спростити вираз 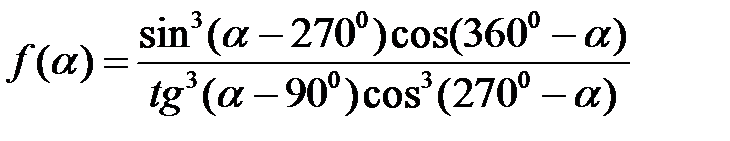 .
.
Розв’язання. Для отримання розв’язку скористаємося формулами зведення (див. табл. 2.1) та властивостями парності й непарності тригонометричних функцій. Маємо
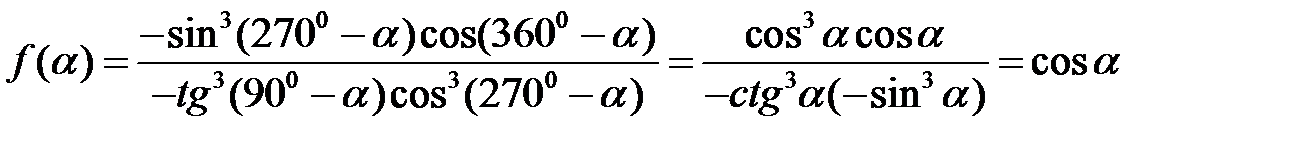 .
. 
Приклад 2.5. Обчислити число 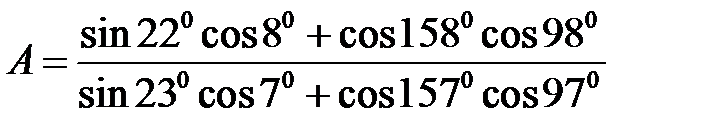 .
.
Розв’язання. Для отримання розв’язку скористаємося формулами зведення (див. табл. 2.1) та формулами додавання. Маємо
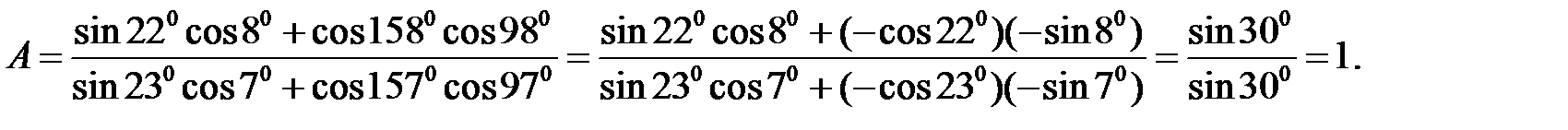
Приклад 2.6. Обчислити 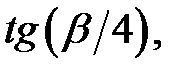 якщо
якщо 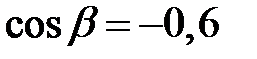 і
і 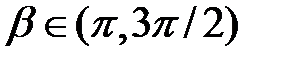 .
.
Розв’язання. Скористаємося формулами 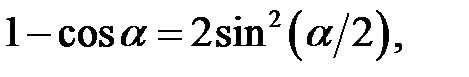
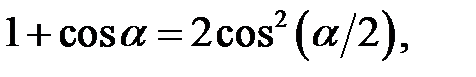 і візьмемо
і візьмемо 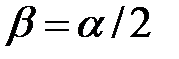 . Маємо
. Маємо 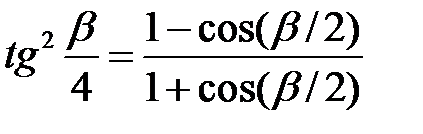 , і задача зводиться до обчислення
, і задача зводиться до обчислення 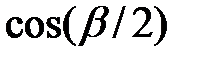 . Проведемо ці обчислення:
. Проведемо ці обчислення:
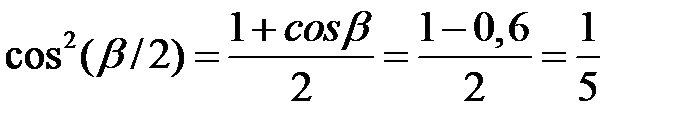 ; оскільки
; оскільки  , то
, то 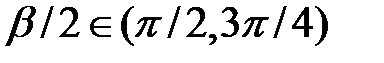 і тому
і тому 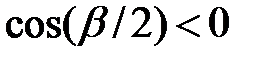 . Значить,
. Значить, 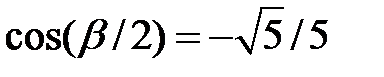 . Таким чином,
. Таким чином, 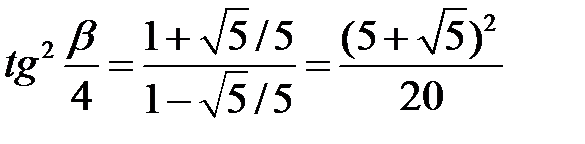 . Кут
. Кут 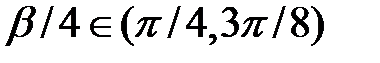 , тому
, тому 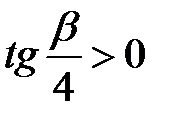 і
і 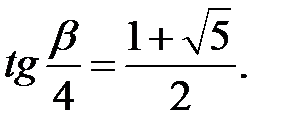
Приклад 2.7. Обчислити 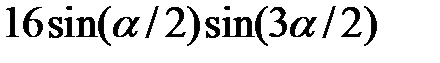 , якщо
, якщо 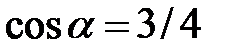 .
.
Розв’язання. Скористаємося формулою перетворення добутку тригонометричних функцій 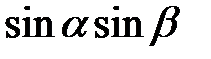 в суму і формулою подвійного аргументу для
в суму і формулою подвійного аргументу для 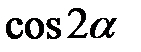 . Маємо
. Маємо
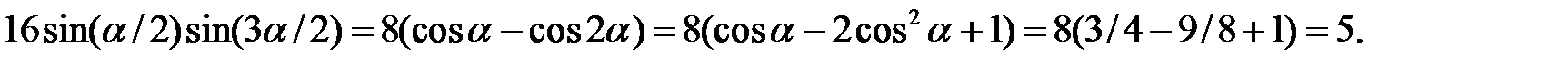
Приклад 2.8. Довести рівність 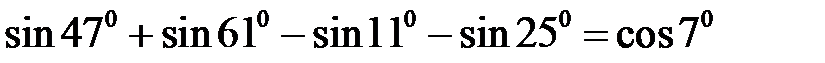 .
.
Розв’язання. Скористаємося формулами для перетворення суми і різниці синусів 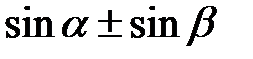 у добуток, а також формулами подвійного аргументу для
у добуток, а також формулами подвійного аргументу для  і
і  . Маємо
. Маємо
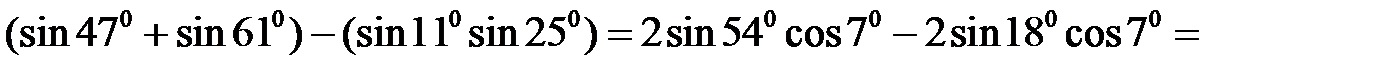
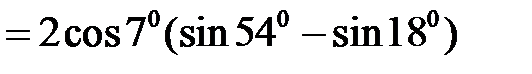
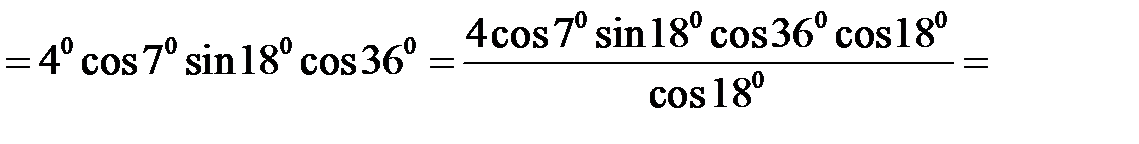

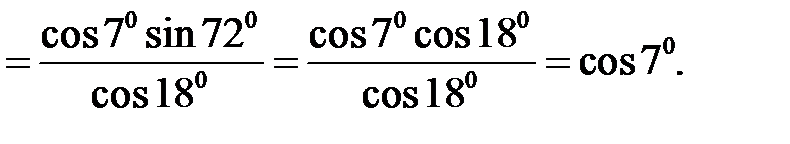
Приклад 2.9. Обчислити 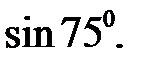
Розв’язання. Скористаємося формулою для синуса суми двох аргументів і табличними значеннями тригонометричних функцій. Маємо
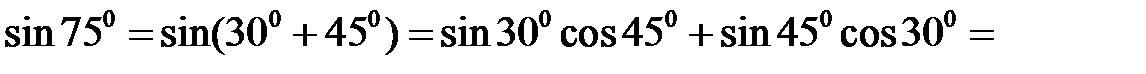
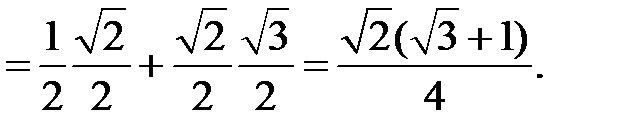
Приклад 2.10. Довести тотожність 
Розв’язання. У лівій частині наведеної рівності виділимо повний куб і квадрат. Маємо
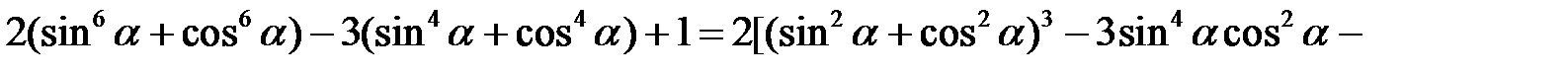
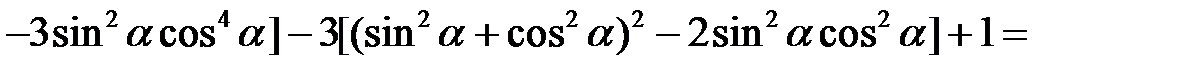
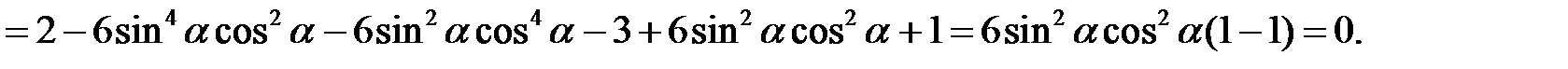 Приклад 2.11. Довести тотожність
Приклад 2.11. Довести тотожність 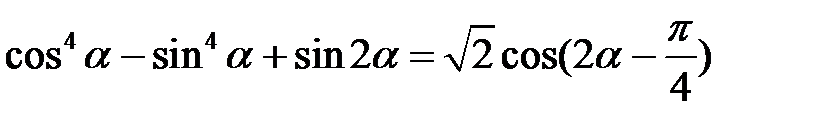 .
.
Розв’язання. До лівої частини рівності застосуємо формулу різниці квадратів, а до правої – формулу косинуса різниці двох аргументів. Маємо
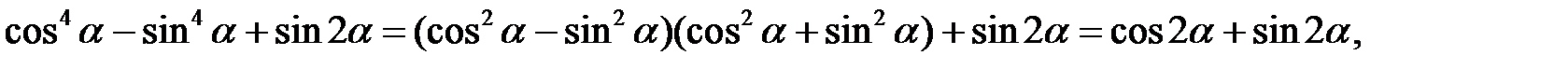
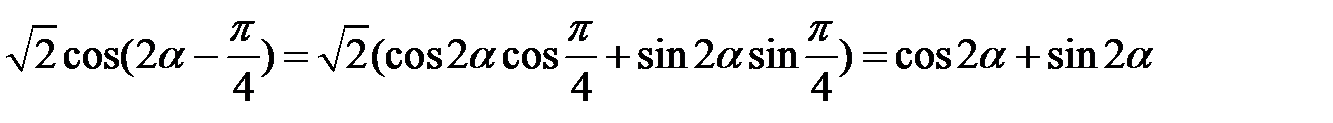 .
.
Ліву та праву частини запропонованої рівності зведено до однакового вигляду, тому вони рівні.
Приклад 2.12. Довести тотожність 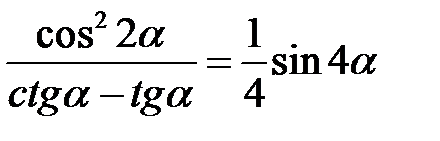 .
.
Розв’язання. 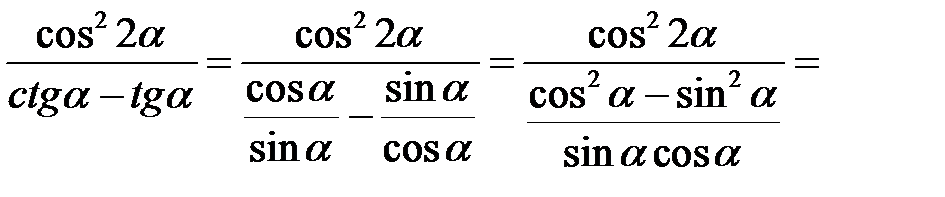
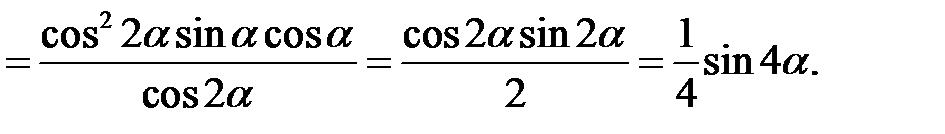
У перетвореннях тригонометричних виразів застосовувалися формули подвійного аргументу для 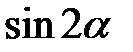 і
і 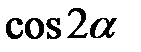 . Слід звернути увагу на те, що наведені дії можливі лише тоді, коли
. Слід звернути увагу на те, що наведені дії можливі лише тоді, коли 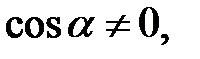
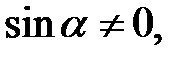
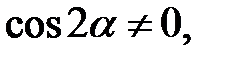 тобто
тобто 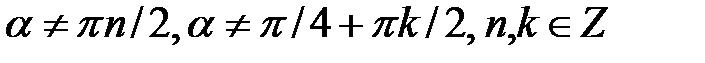 , або
, або 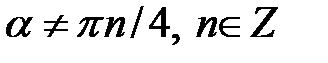 .
.
Приклад 2.13. Довести тотожність 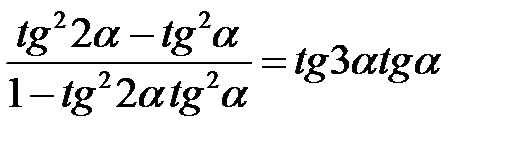 .
.
Розв’язання. Розкладемо на множники ліву частину рівності та застосуємо формули тангенса суми і різниці двох аргументів. Маємо
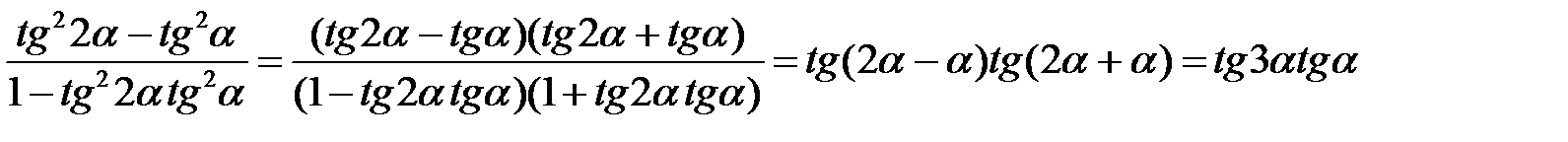 .
.
Доведена тотожність виконується, якщо 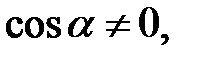
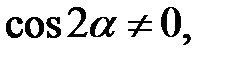
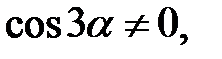
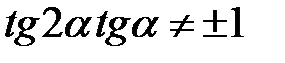 , тобто
, тобто 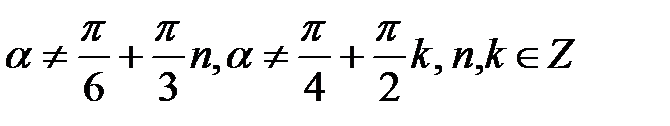 .
.
Приклад 2.14. Довести числову рівність 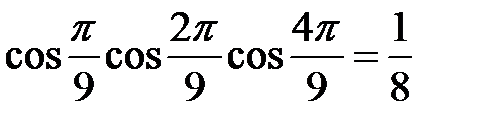 .
.
Розв’язання. Помножимо та поділимо ліву частину рівності на 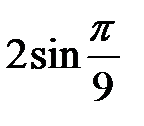 і скористаємося формулами подвійного аргументу. Маємо
і скористаємося формулами подвійного аргументу. Маємо
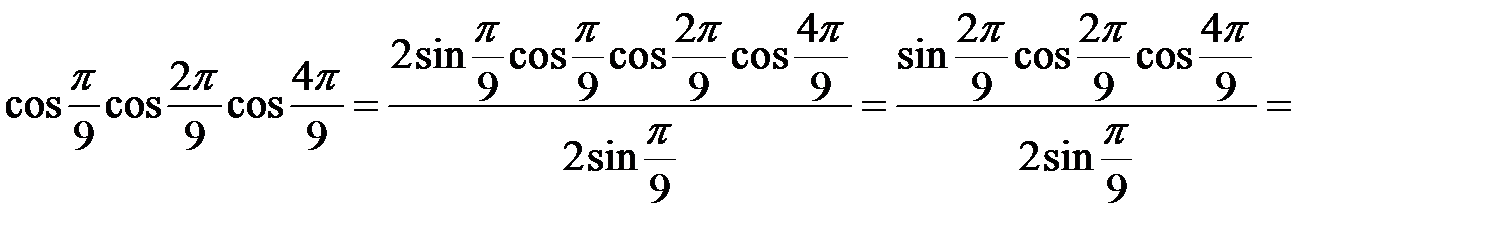
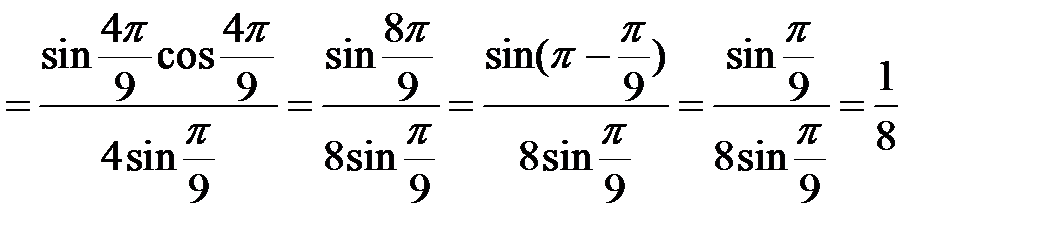 .
.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 952; Нарушение авторских прав?; Мы поможем в написании вашей работы!