
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тригонометричні функції числового аргументу
|
|
|
|
Розділ 2. ТРИГОНОМЕТРИЧНІ ПЕРЕТВОРЕННЯ
Завдання для самостійної роботи
1.14. Спростити:
a) 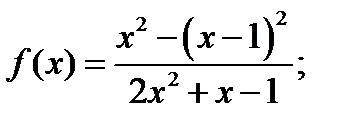 b)
b) 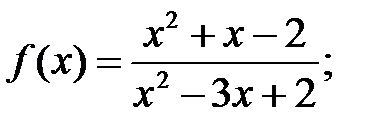 c)
c) 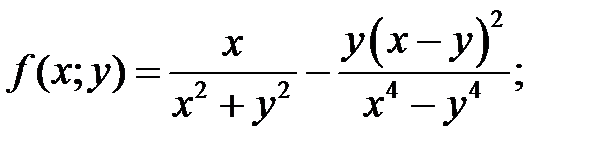
d) 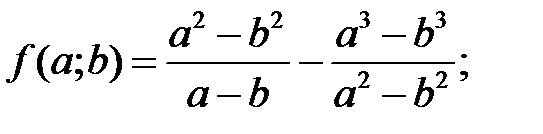 e)
e) 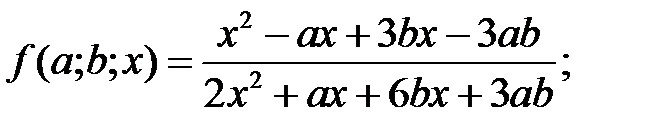 f)
f) 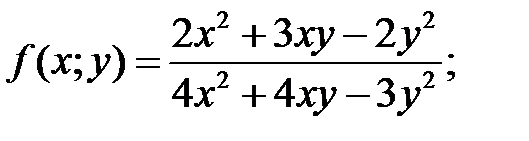 g)
g) 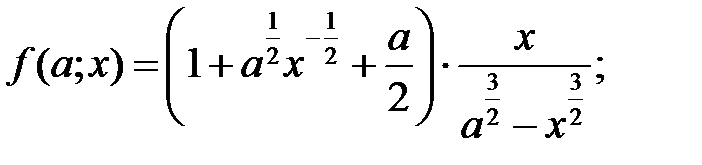 h)
h) 
i) 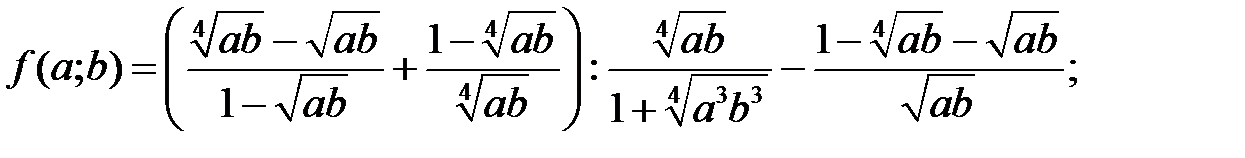
j) 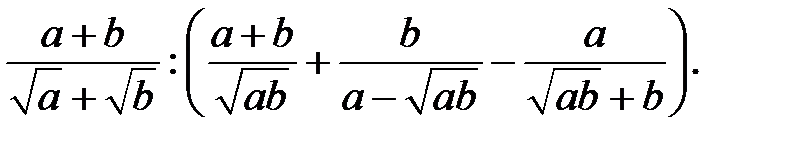
1.15. Розкласти дріб 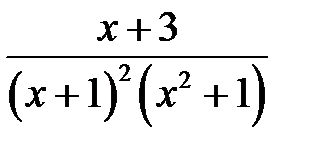 на суму елементарних дробів.
на суму елементарних дробів.
1.16. Розкласти дріб 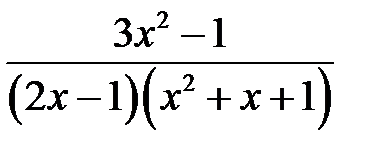 на суму елементарних дробів.
на суму елементарних дробів.
Наведемо означення тригонометричних функцій числового аргументу.
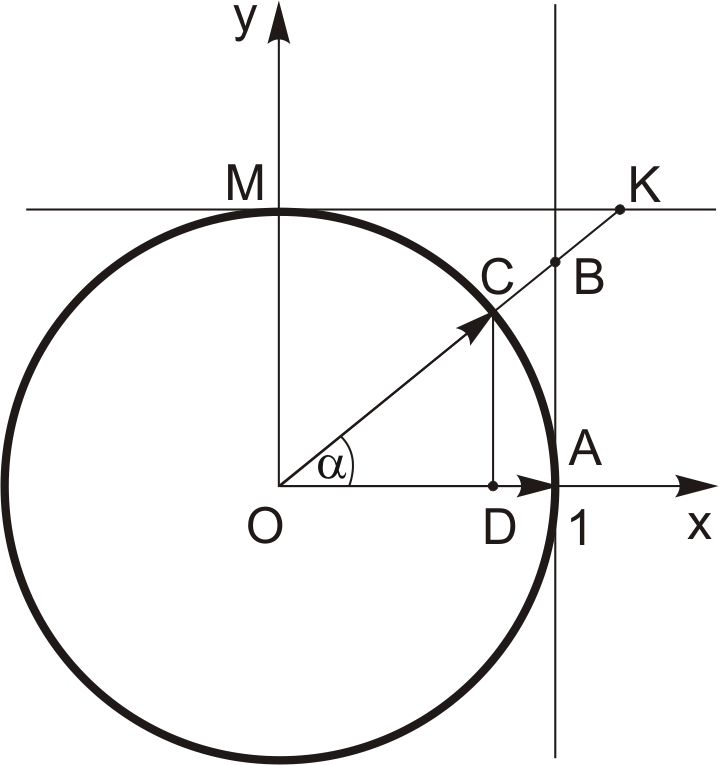 Синусом числа
Синусом числа 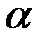 (
(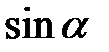 ) називається ордината точки C, яка утворюється в результаті повороту радіус-вектора
) називається ордината точки C, яка утворюється в результаті повороту радіус-вектора 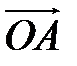 = {0,1} на кут
= {0,1} на кут 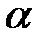 радіан. Якщо
радіан. Якщо 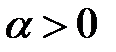 , то поворот здійснюється проти ходу годинникової стрілки і вважається додатним, а якщо
, то поворот здійснюється проти ходу годинникової стрілки і вважається додатним, а якщо 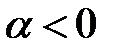 , то поворот – від’ємний і здійснюється за ходом годинникової стрілки.
, то поворот – від’ємний і здійснюється за ходом годинникової стрілки.
Косинусом числа  (
(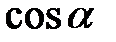 ) називається абсциса точки С.
) називається абсциса точки С.
Тангенсом числа 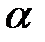 (
(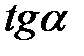 ) називається ордината точки В, яка розташована на перетині продовження радіус-вектора
) називається ордината точки В, яка розташована на перетині продовження радіус-вектора 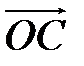 з віссю тангенсів (пряма, проведена через точку А(1,0) перпендикулярно до осі ОХ).
з віссю тангенсів (пряма, проведена через точку А(1,0) перпендикулярно до осі ОХ).
Котангенсом числа 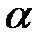 (
(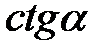 ) називається Рис. 2.1
) називається Рис. 2.1
абсциса точки К, яка лежить на перетині продовження радіус-вектора 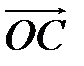 з віссю котангенсів (пряма, проведена через точку М(0,1) перпендикулярно до осі ОY).
з віссю котангенсів (пряма, проведена через точку М(0,1) перпендикулярно до осі ОY).
Іноді використовуються ще дві тригогонометричні функції, а саме секанс числа 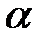 (
(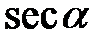 ) і косеканс числа
) і косеканс числа 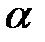 (
( ). Ці функції вводяться таким чином:
). Ці функції вводяться таким чином:
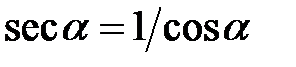 ,
, 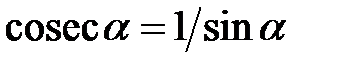 .
.
Між тригонометричними функціями кута 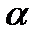 існують прості співвідношення:
існують прості співвідношення:
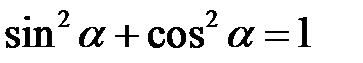 ;
; 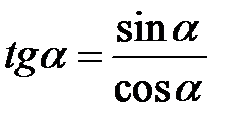 ,
, 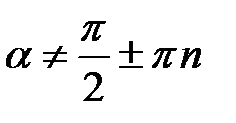 ;
;
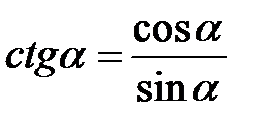 ,
, 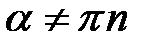 ;
; 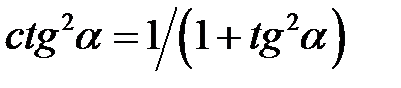 ,
, 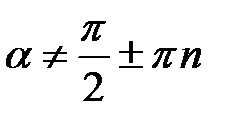 ;
;
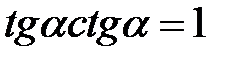 ,
, 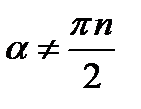 ;
; 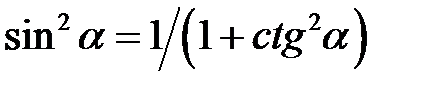 ,
, 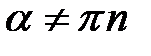 .
.
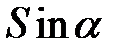 набуває додатних значень у першій (
набуває додатних значень у першій (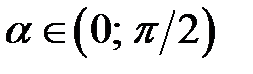 ) та другій (
) та другій (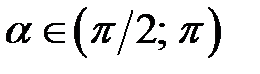 ) чвертях і від’ємних – у третій (
) чвертях і від’ємних – у третій ( ) та четвертій (
) та четвертій (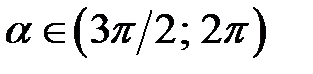 );
); 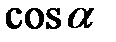 набуває додатних значень у першій та четвертій чвертях і від’ємних – у другій та третій;
набуває додатних значень у першій та четвертій чвертях і від’ємних – у другій та третій; 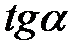 і
і  – додатних у першій та третій чвертях і від’ємних – у другій та четвертій (рис. 2.2).
– додатних у першій та третій чвертях і від’ємних – у другій та четвертій (рис. 2.2).
Згідно з означенням тригонометричних функцій мають місце такі формули:
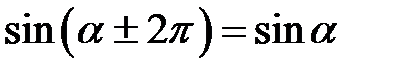 ,
, 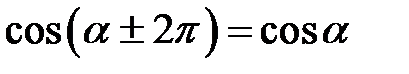 ,
, 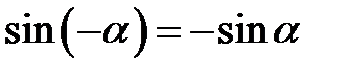 ,
,
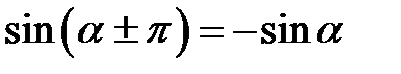 ,
, 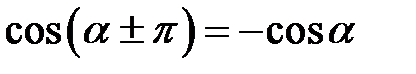 ,
, 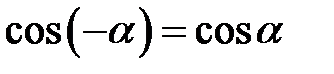
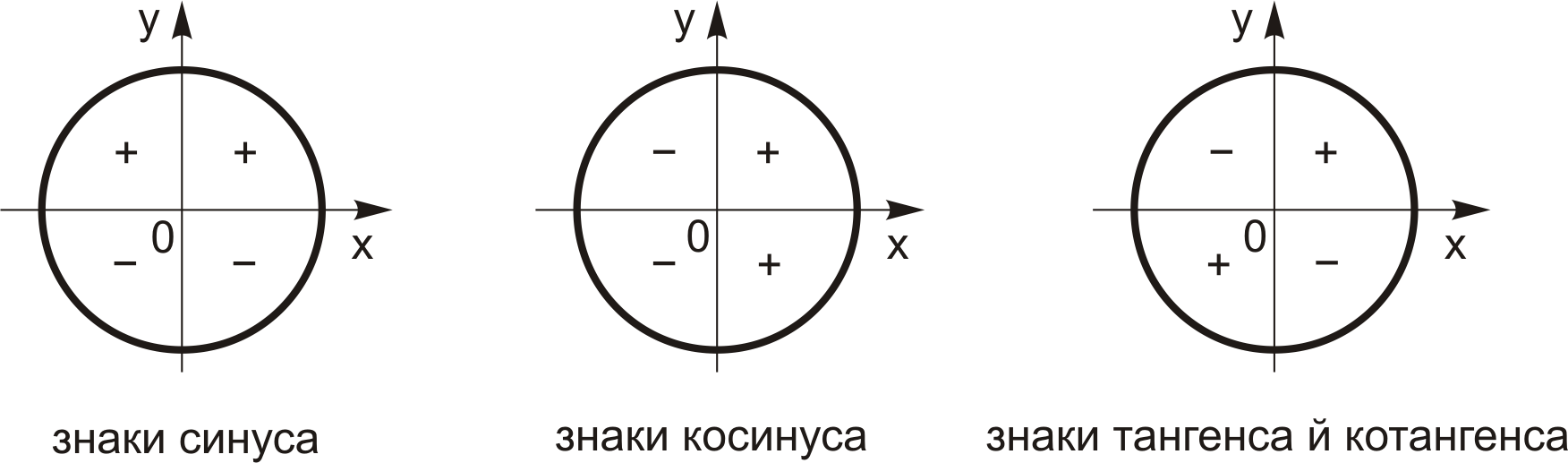
Рис. 2.2
для будь-якого значення 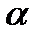 і
і
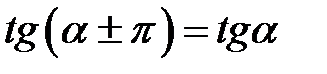 ,
,  ,
, 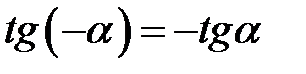 ,
, 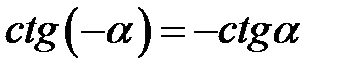
для будь-якого допустимого значення 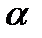 .
.
Табличні значення тригонометричних функцій гострих кутів наведено в табл. 2.1.
Таблиця 2.1
| Функція | Кут 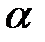 : радіани (градуси) : радіани (градуси)
| ||||
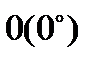
| 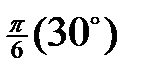
| 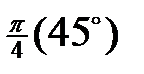
| 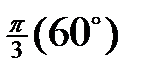
| 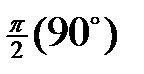
| |
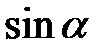
| 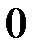
| 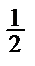
| 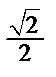
| 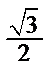
| 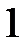
|
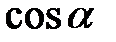
| 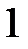
| 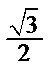
| 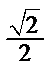
| 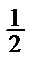
| 
|
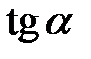
| 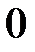
| 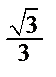
| 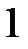
| 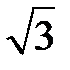
| – |
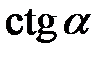
| – | 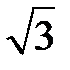
| 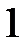
| 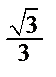
| 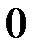
|
Приклад 2.1. Визначити знаки таких виразів: а)  б)
б) 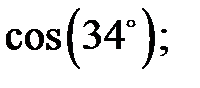
в) 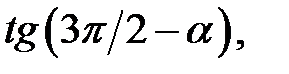 де
де 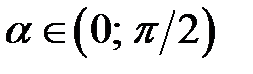 .
.
Розв’язання: а) кут 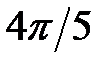 належить другій чверті, тому
належить другій чверті, тому  ; б) кут
; б) кут  належить першій чверті, тому
належить першій чверті, тому 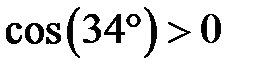 ; в) значення кута
; в) значення кута 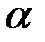 не перевищує
не перевищує 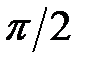 , тому вираз
, тому вираз 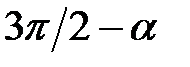 належить другій чверті. Синус і косинус кутів другої чверті мають різні знаки, тому
належить другій чверті. Синус і косинус кутів другої чверті мають різні знаки, тому 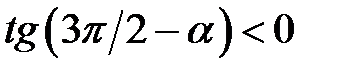 .
.
Приклад 2.2. Обчислити 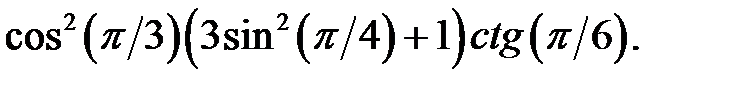
Розв’язання. Аргументи тригонометричних функції – табличні. Значення тригонометричних функцій від цих аргументів – відомі, а саме:

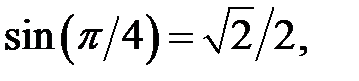
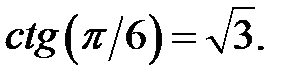
Тому 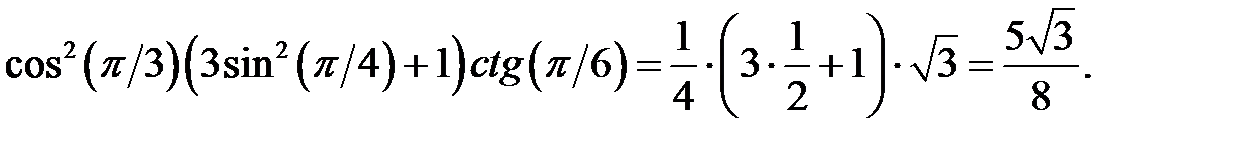
Приклад 2.3. Обчислити 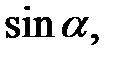
 ,
, 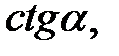 якщо
якщо 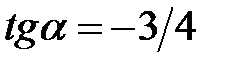 і
і 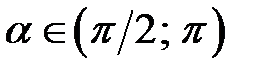 .
.
Розв’язання. Оскільки 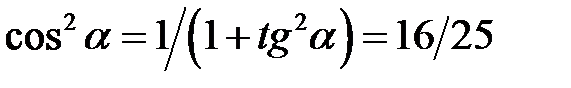 , то
, то 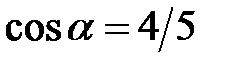 або
або 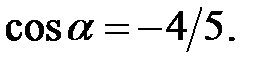 Оскільки
Оскільки 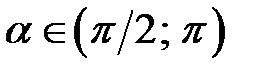 , то
, то 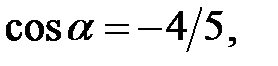
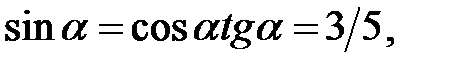
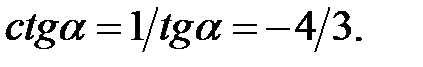
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 625; Нарушение авторских прав?; Мы поможем в написании вашей работы!