
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Раціональних дробів на прості дроби
Елементарні формули алгебри. Спрощення алгебраїчних виразів. Раціональні дроби. Розкладання правильних
Завдання для самостійної роботи
1.11. Розв’язати квадратні рівняння за теоремою Вієта:
1) 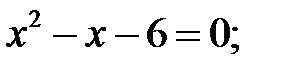 2)
2) 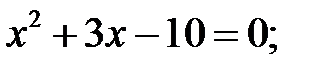 3)
3) 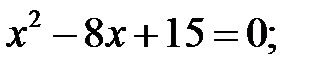 4)
4) 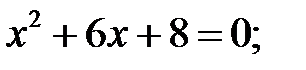
5)  6)
6) 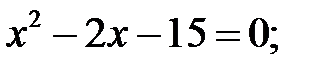 7)
7) 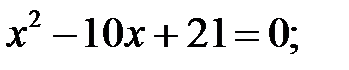 8)
8) 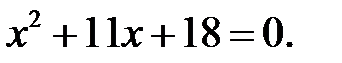
1.12. Знайти дійсні корені многочленів:
1) 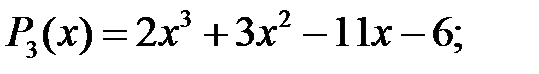 2)
2) 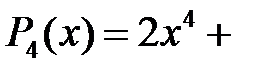

3)  4)
4) 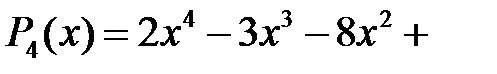
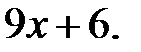
1.13. Розв’язати рівняння в області дійсних чисел:
1) 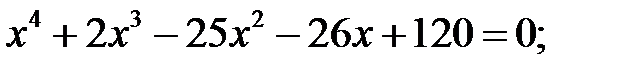 2)
2) 
3) 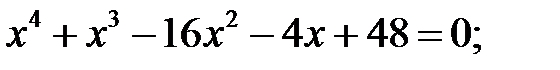 4)
4) 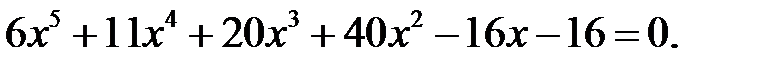
Означення 1. Дріб вигляду  , де
, де 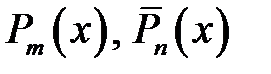 – многочлени, називається раціональним; якщо
– многочлени, називається раціональним; якщо 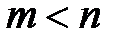 , то раціональний дріб є правильним.
, то раціональний дріб є правильним.
Означення 2. Раціональні дроби 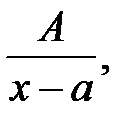
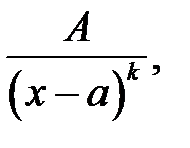
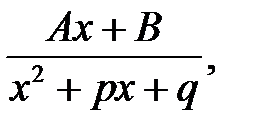
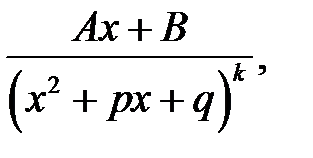 де
де 
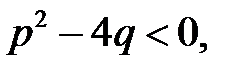 називаються елементарними.
називаються елементарними.
Має місце твердження: правильний раціональний дріб можна зобразити у вигляді суми елементарних дробів. Зокрема, справедливо,що
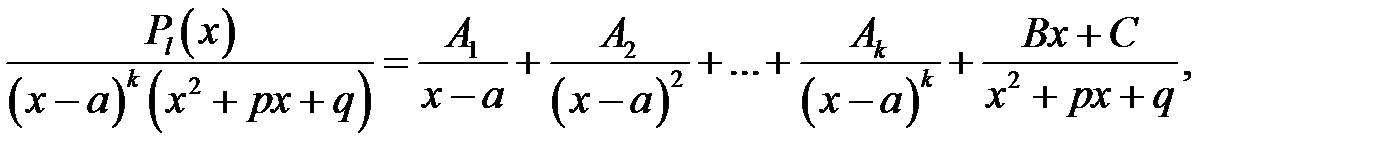
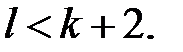
Для знаходження коефіцієнтів 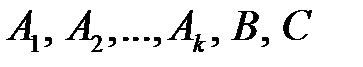 праву частину зводять до загального знаменника і порівнюють чисельники дробів у лівій і правій частинах одержаної рівності, потім комбінують методи:
праву частину зводять до загального знаменника і порівнюють чисельники дробів у лівій і правій частинах одержаної рівності, потім комбінують методи:
1) підставляють ліворуч і праворуч одні і ті ж числа (зазвичай корені знаменника);
2) прирівнюють коефіцієнти при однакових степенях 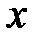 ліворуч і праворуч рівності і розв’язують отриману систему.
ліворуч і праворуч рівності і розв’язують отриману систему.
Формули скороченого множення і ділення:

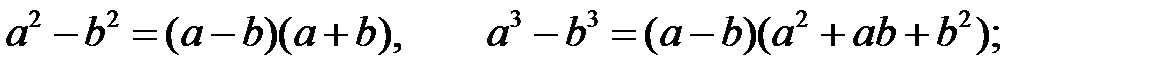

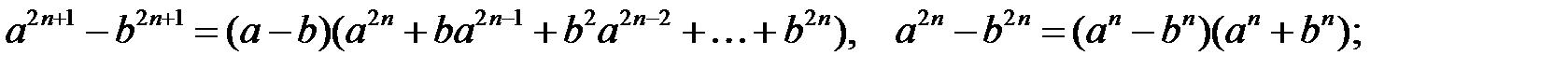
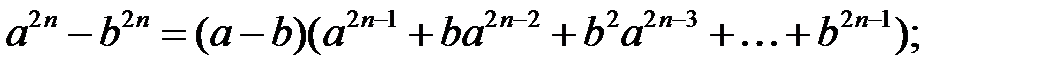
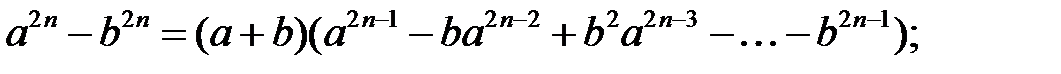
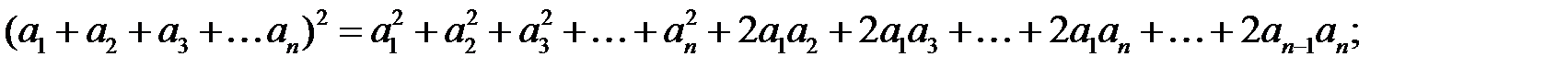
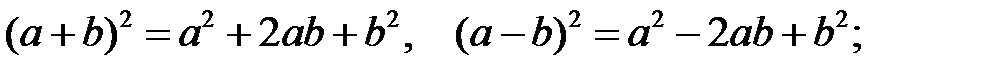
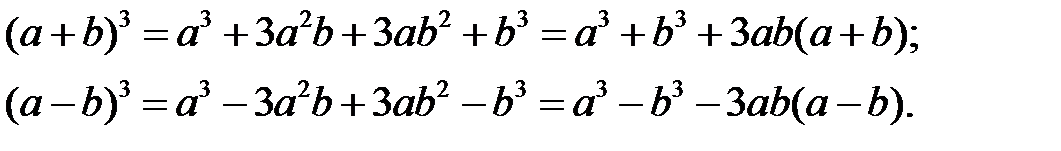
Формула бінома Ньютона:
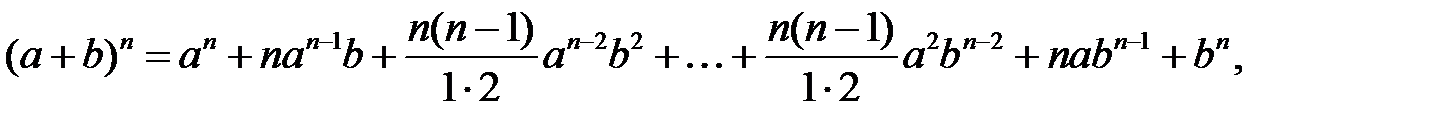
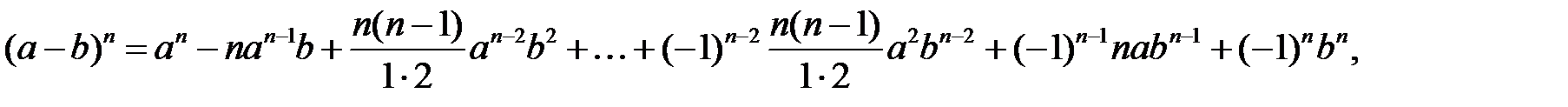 де
де 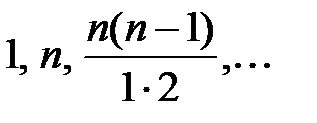 – біноміальні коефіцієнти, які знаходяться в
– біноміальні коефіцієнти, які знаходяться в  –му рядку «трикутника Паскаля».
–му рядку «трикутника Паскаля».
Алгоритм побудови «трикутника Паскаля» (табл. 1.1): кожний елемент наступного рядка, окрім його крайніх елементів, дорівнює сумі двох сусідніх з ним елементів попереднього рядка; крайні елементи кожного рядка є одиниці.
Таблиця 1.1
| Номер рядка | Біноміальні коефіцієнти |
| 1 1 | |
| 1 2 1 | |
| 1 3 3 1 | |
| 1 4 6 4 1 | |
| 1 5 10 10 5 1 | |
| 1 6 15 20 15 6 1 |
Приклад 1. 7. Знайти 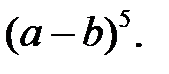
Розв’язання. Коефіцієнти беремо з 5-го рядка, знаки “  ”, “–” чергуємо:
”, “–” чергуємо: 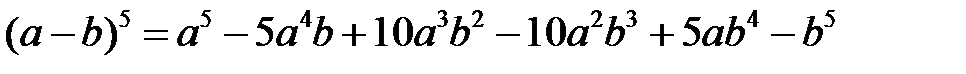 .
.
Формула виділення повного квадрата:
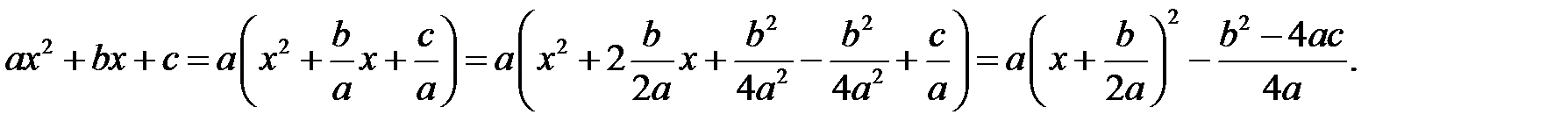
Приклад 1.8. Спростити 
Розв’язання. ОДЗ: 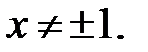
 якщо
якщо 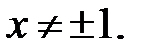
Приклад 1.9. Спростити вираз 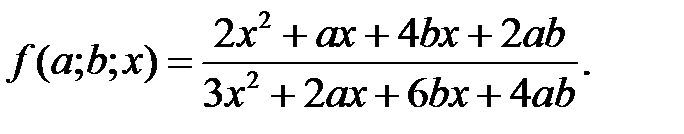
Розв’язання. 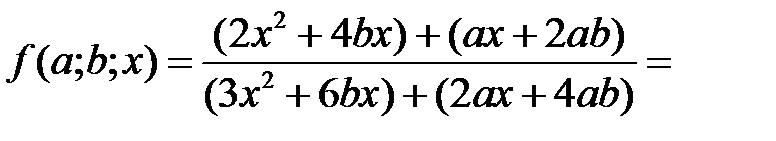
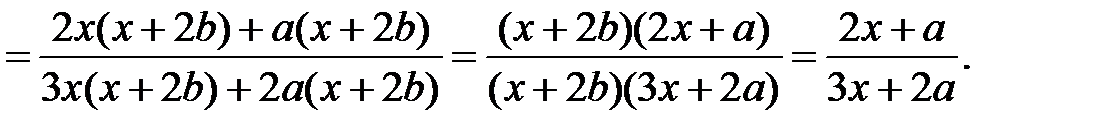
ОДЗ: 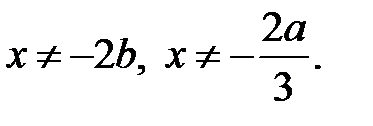
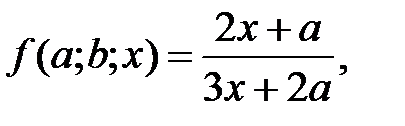 якщо
якщо 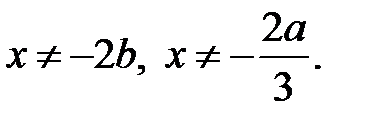
Приклад 1.10. Спростити 
Розв’язання. Позначимо цей вираз через 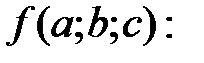
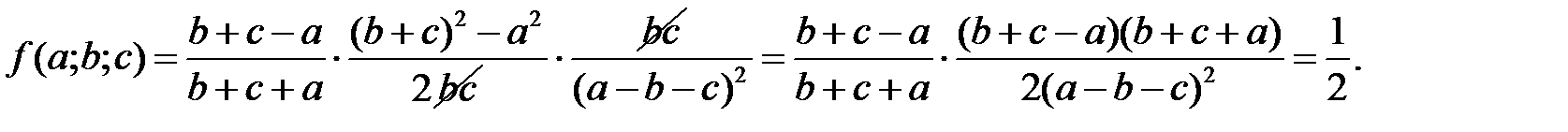
ОДЗ перетворень: 
Приклад 1.11. Спростити вираз 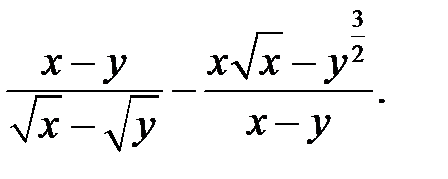
Розв’язання. 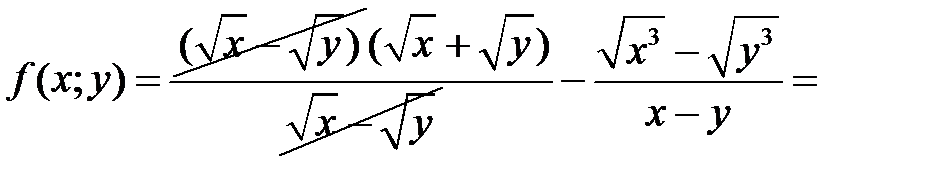

 ,
,
якщо 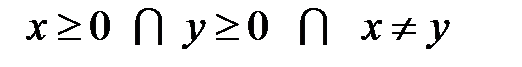 (це ОДЗ перетворень).
(це ОДЗ перетворень).
Приклад 1.12. Спростити вираз

Розв’язання. ОДЗ: 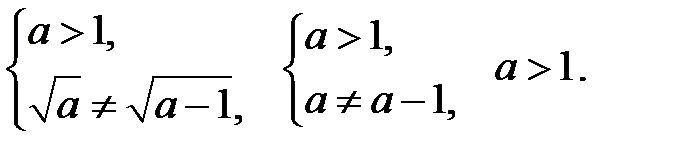
Звільнимося від ірраціональності в знаменнику спочатку першого, а потім другого дробу. Маємо:
1) 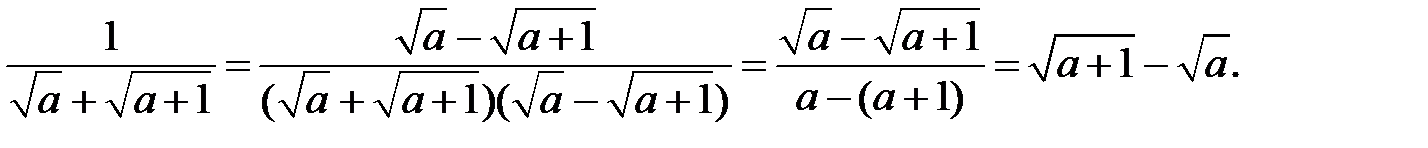
2) 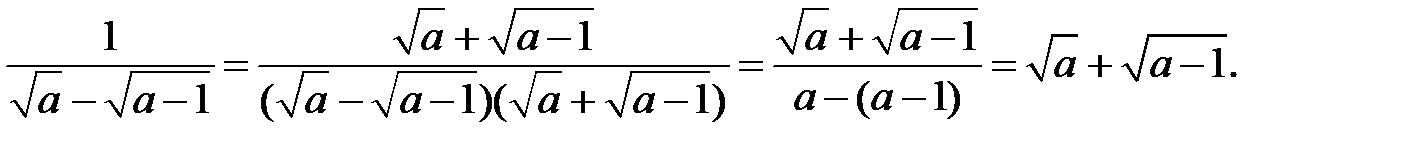
3) 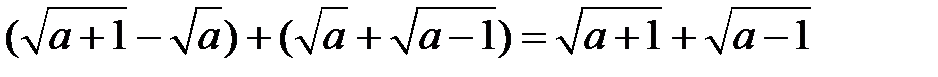 .
.
4) 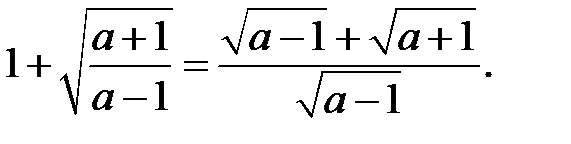
5) 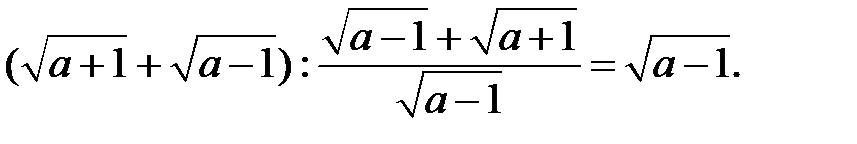
Отже, 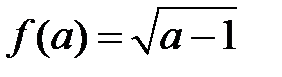 , якщо
, якщо 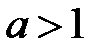 .
.
Приклад 1.13. Знаючи табличні інтеграли 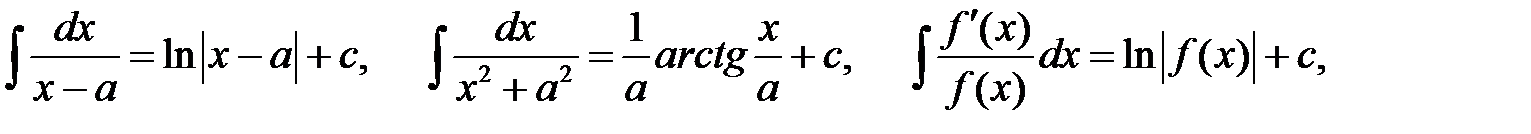
знайти інтеграл 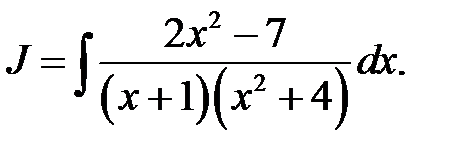
Розв’язання. Розкладемо підінтегральний дріб на елементарні дроби:
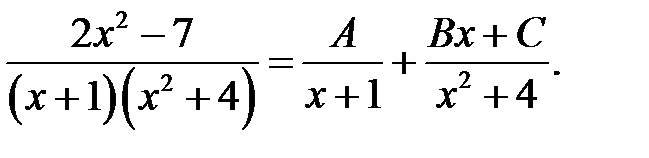
Маємо: 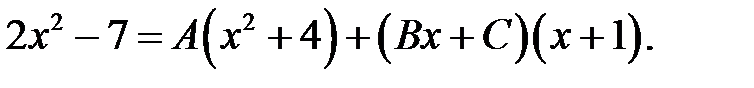 Покладемо
Покладемо 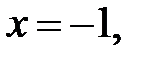 тоді
тоді 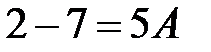 і
і 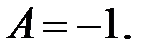
Порівняємо коефіцієнти при однакових степенях:
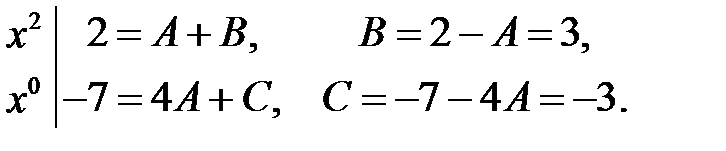
Тоді 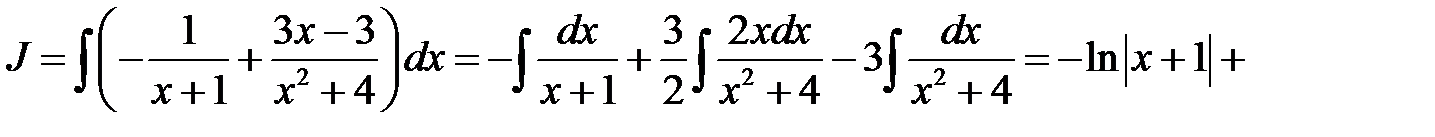

|
|
Дата добавления: 2014-12-26; Просмотров: 716; Нарушение авторских прав?; Мы поможем в написании вашей работы!