
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Завдання для самостійної роботи. Обчислити значення тригонометричних виразів:
|
|
|
|
Обчислити значення тригонометричних виразів:
2.08. 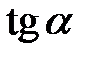 , якщо
, якщо 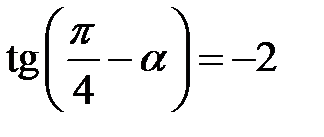 . 2.09.
. 2.09. 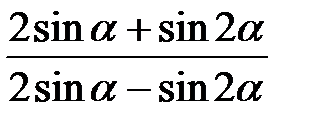 , якщо
, якщо 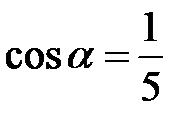 .
.
2.10. 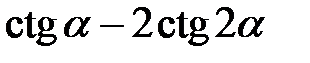 , якщо
, якщо 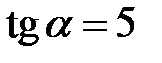 . 2.11.
. 2.11. 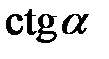 , якщо
, якщо 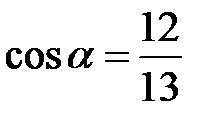 і
і 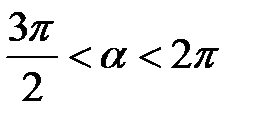 .
.
Спростити:
2.12. 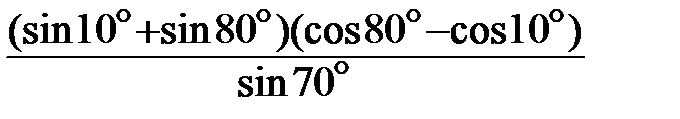 . 2.13.
. 2.13. 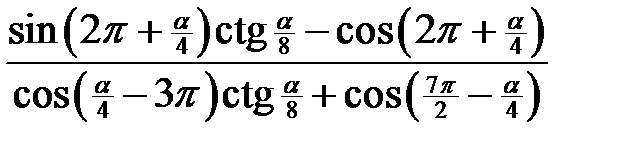 .
.
2.14. 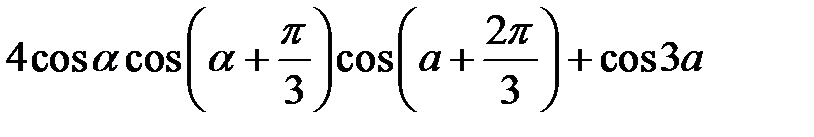 .
.
2.15. 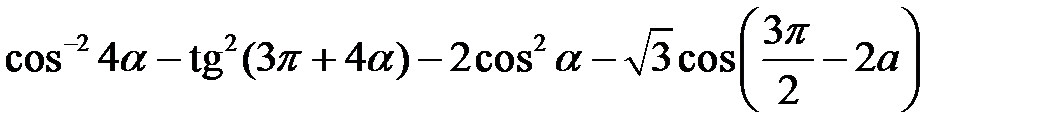 .
.
2.16. 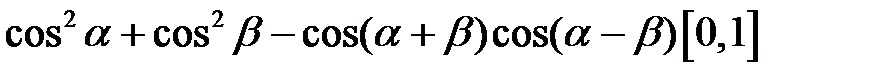 . 2.17.
. 2.17. 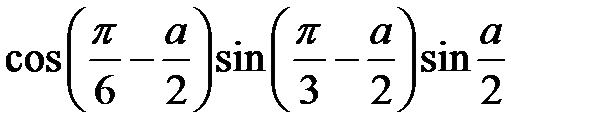 .
.
Довести тотожності:
2.18. 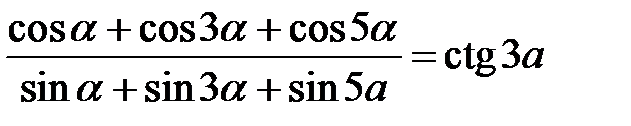 . 2.19.
. 2.19. 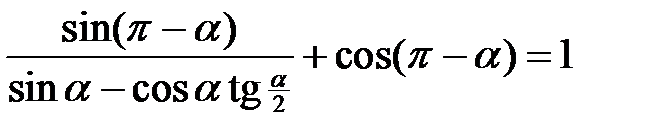 .
.
2.20. 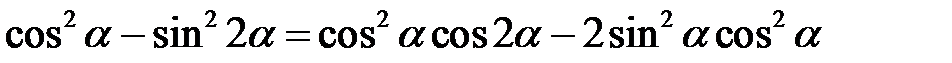 .
.
2.21. 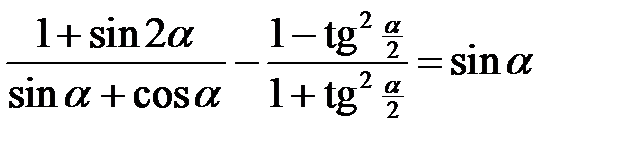 . 2.22.
. 2.22. 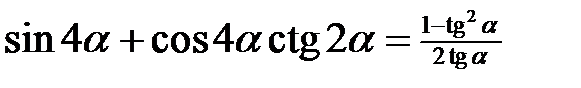 .
.
2.23. 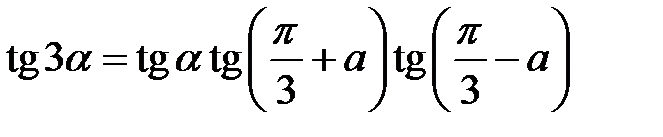 . 2.24.
. 2.24. 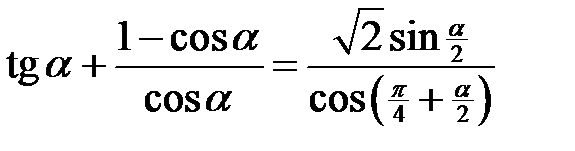 .
.
2.25. 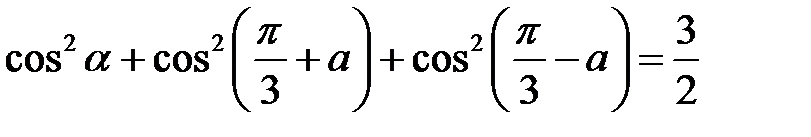 . 2.26.
. 2.26. 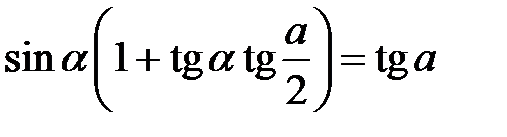 .
.
З’ясувати, для яких значень 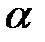 мають місце рівності:
мають місце рівності:
2.27. 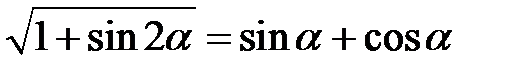 . 2.28.
. 2.28. 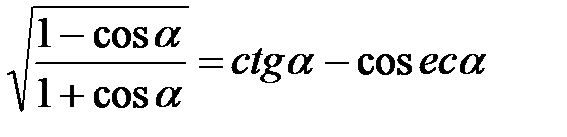 .
.
У подальшому нам знадобиться означення ще чотирьох функцій числового аргументу.
Нехай число 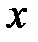 належить проміжку
належить проміжку 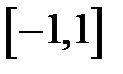 . Арксинусом числа
. Арксинусом числа 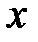 (
(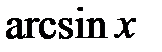 ) називається таке число
) називається таке число 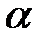 (або така дуга
(або така дуга 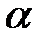 , або такий кут
, або такий кут 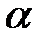 ) із відрізка
) із відрізка  , синус якого дорівнює
, синус якого дорівнює 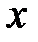 . Таким чином, запис
. Таким чином, запис 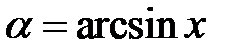 означає, що
означає, що 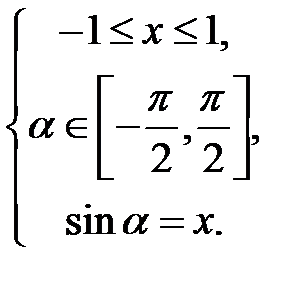
Арккосинусом числа 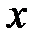 (
( ) називається таке число
) називається таке число 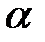 (або така дуга
(або така дуга 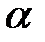 , або такий кут
, або такий кут 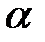 ) із відрізка
) із відрізка 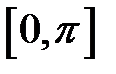 , косинус якого дорівнює
, косинус якого дорівнює 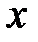 . Отже, запис
. Отже, запис 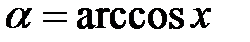 означає, що
означає, що 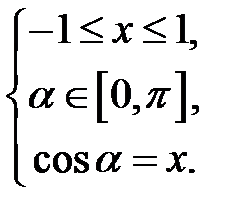
Нехай 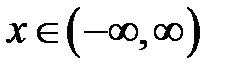 . Арктангенсом числа
. Арктангенсом числа 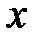 називається таке число
називається таке число 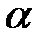 (або така дуга
(або така дуга 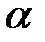 , або такий кут
, або такий кут 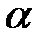 ) із інтервалу
) із інтервалу 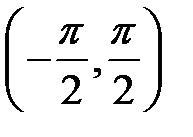 , тангенс якого дорівнює числу
, тангенс якого дорівнює числу 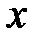 . Аналогічно попереднім записам маємо:
. Аналогічно попереднім записам маємо: 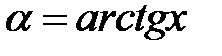 означає, що
означає, що 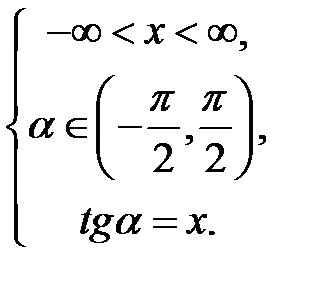
Арккотангенсом числа 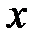 називається таке число
називається таке число 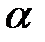 (або така дуга
(або така дуга 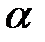 , або такий кут
, або такий кут 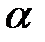 ) із інтервалу
) із інтервалу 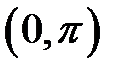 , котангенс якого дорівнює
, котангенс якого дорівнює 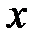 . Отже,
. Отже, 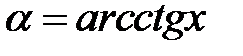 означає, що
означає, що 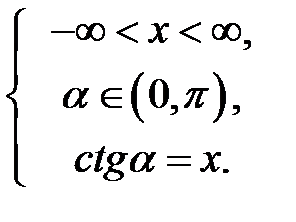
Корисною є табл. 2.2 найпростіших значень функцій.
Таблиця 2.2
| Функція | Аргумент | ||||||
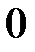
| 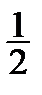
| 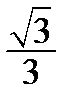
| 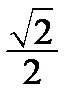
| 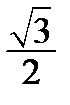
| 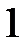
| 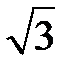
| |
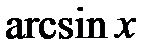
| 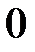
| 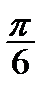
| 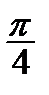
| 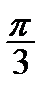
| 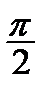
| – | |

| 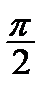
| 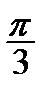
| 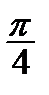
| 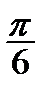
| 
| – | |
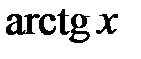
| 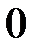
| 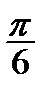
| 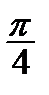
| 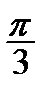
| |||
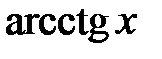
| 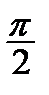
| 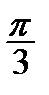
| 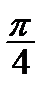
| 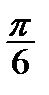
|
Зауваження. Позначення функцій пов’язано зі змістом слова «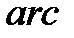 »- «арка», або «дуга».
»- «арка», або «дуга».
Наведемо деякі тотожності, зв’язані із 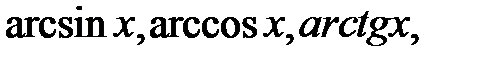
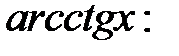
1) 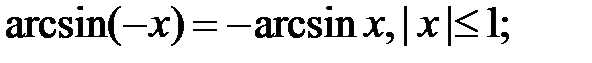 2)
2) 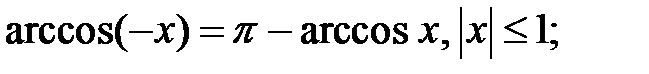
3) 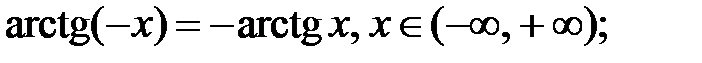 4)
4) 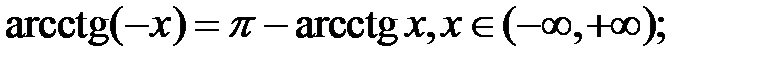
5) 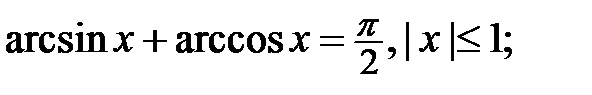 6)
6) 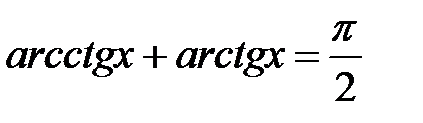 .
.
Приклад 2.15. Обчислити 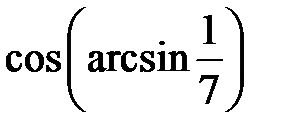 .
.
Розв’язання. Треба знайти 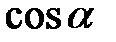 , якщо відомо, що
, якщо відомо, що 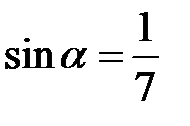 . Кут
. Кут 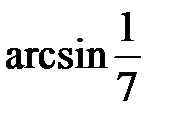 розташований у першій чверті і має додатний косинус. Тому
розташований у першій чверті і має додатний косинус. Тому 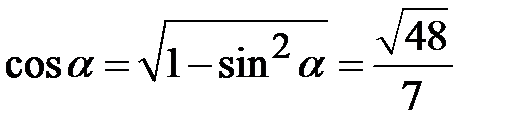 .
.
Приклад 2.16. Обчислити 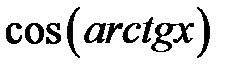 .
.
Розв’язання. За формулою 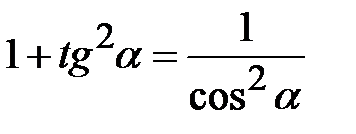 знайдемо
знайдемо 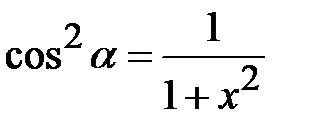 . Важливо зауважити, що за означенням арктангенса цей кут розташований у першій або четвертій чверті і має додатне значення косинуса, тобто
. Важливо зауважити, що за означенням арктангенса цей кут розташований у першій або четвертій чверті і має додатне значення косинуса, тобто 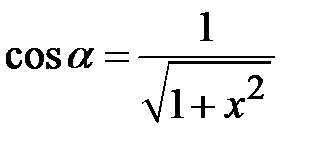 .
.
Приклад 2.17. Обчислити 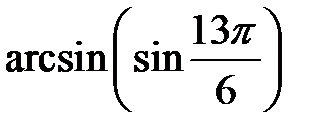 .
.
Розв’язання. Оскільки 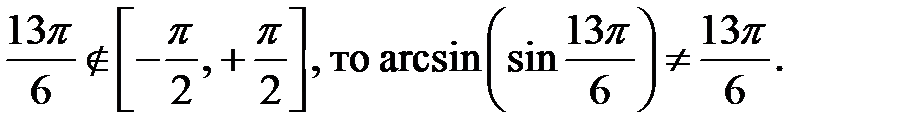 За допомогою формул зведення
За допомогою формул зведення 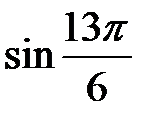 перетворюється на
перетворюється на 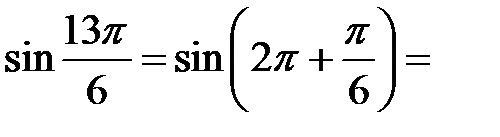
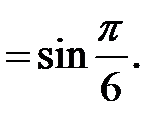 Аргумент
Аргумент 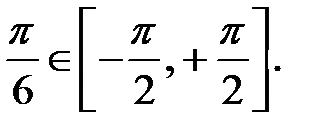 Остаточно
Остаточно 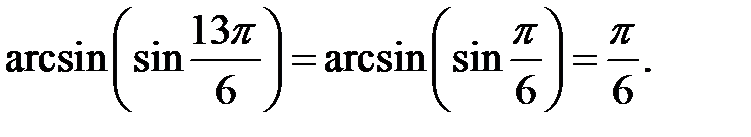
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 565; Нарушение авторских прав?; Мы поможем в написании вашей работы!