Вопросы для самопроверки. Примеры решения задач

Примеры решения задач.

Задача 1. Исследовать сходимость ряда:

Решение: Применим признак Даламбера:

Т.к. l > 1, то ряд расходится.

Задача 2. Исследовать сходимость ряда .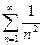

Решение: Имеем 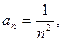следовательно, 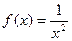-непрерывная, положительная и монотонно убывающая функция при x ≥ 1. Применим интегральный признак сходимости.

Несобственный интеграл сходится (является конечной величиной), поэтому сходится и данный ряд.

1. Какое выражение называется числовым рядом с положительными членами?

Знакочередующимся числовым рядом?

2. Что понимается под суммой сходящегося числового ряда?

3. Можно ли утверждать, что ряд сходится, если предел его общего члена равен нулю при n® ¥?

4. В чём состоит признак Даламбера?

5. Какие знакопеременные числовые ряды называются абсолютно сходящимися и какие условно сходящимися?

6. В чём заключается интегральный признак сходимости числового ряда?

7. Сформулировать один из признаков сравнения числовых рядов.

Тема 15. Степенные ряды. Приложения степенных рядов.

Пискунов, гл XVI, § 9-22, упр 40-132

Данко ч. II, гл. III, §2-6.

15. 1. Основные понятия и формулы.

1. Определение. Функциональный ряд вида a₀+a₁(x-x₀)+a ₂ (x-x₀) ² +

+…++… где a _0, a _{1 …} a _n – действительные числа (коэффициенты степенного ряда) называется степенным рядом. a ₀ +a ₁ x+ a ₂ x² +a ₃ x³ + + …+a_n xⁿ +… частный случай степенного ряда.

2. - формула для нахождения радиуса сходимости сте-пенного ряда.

3. Интервал сходимости можно находить, применяя непосредственно признак Даламбера или признак Коши:

или,

где U_n=a_n(x-x ₀ )ⁿ или U_n=a_n xⁿ

4. Всякая функция f(x), бесконечно дифференцируемая в интервале

(x ₀ -R,x ₀ +R), может быть разложена в ряд Тейлора:

или в ряд Маклорена:

5. На практике часто приходится прибегать к приближённым вычислениям, основанным на разложении некоторой функции в степенной ряд и последующей замене ряда конечной суммой с требуемой точностью. При вычислении определённых интегралов, решении дифференциальных уравнений также применяют разложение соответствующих функций в степенные ряды.

15.2. Примеры решения задач.

Задача 1. Найти область сходимости степенного ряда

Решение: Данный степенной ряд можно записать так:

(1)

Применяем признак Даламбера:

Как видно, ряд будет сходиться для тех значений х,для которых

илиили

Выясним вопрос о сходимости ряда на концах интервала. При ряд (1) примет вид:

(2)

Ряд (2) является знакочередующимся; его общий член по абсолютному значению стремится к нулю при n ®¥. По признаку Лейбница о сходимости знакочере­дующихся рядов заключаем, что ряд (2) сходится. Сле­довательно, значение принадлежит области схо­димости данного ряда.

Подставив в (1), получим: (3)

Ряд (3) расходится (для этого достаточно сравнить его с гармоническим рядом). Следовательно, значение не принадлежит области сходимости данного ряда. Таким образом, — область

сходимости исследуемого ряда.

Задача 2. Вычислить интеграл с точностью до 0,001.

Решение: Предварительно представим подынтег­ральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции sin х, будем иметь:

Тогда

Мы получили знакочередующийся ряд, который удовлет­воряет условиям теоремы Лейбница. Так как в получен­ном ряде четвертый член по абсолютному значению меньше 0,001, то ограничиваемся только

первыми тремя членами.

Итак,

Задача 3. Найти первые три (отличные от нуля) члена разложения в ряд Маклорена функции у(х), яв­ляющейся частным решением дифференциального урав­нения у' =x+ х ² — y ² + cos x, если у( 0 )= 1.

Решение: Положим, что y(x) является решением данного дифференциального уравнения при указанных начальных условиях. Если y(x) допускает разложение в ряд Маклорена, то имеем:

(1)

Свободный член разложения (1), т.е. y (0), дан по условию. Чтобы найти значения (0), (0), (0),…,можно данное уравнение последо-вательно дифференцировать по переменной x и затем вычислить значения производных при x =0.

Значение y¢(0) получаем, подставив начальные условия в данное уравнение:

y¢ (0)=0+0-1+1=0; y¢ (0)=0

y¢¢ (x)=1+2 x -2 yy¢ -sin x - производная данного уравнения (2)

y¢¢ (0)=1+0-0-0=1;

y¢¢¢(x) =2-2(y¢)²-2 yy¢¢- cos x - производная уравнения

y¢¢¢ (0)=2-0-2-1= -1.

…………………..

Подставив найденные значения производных при x =0 в (1), получим разложение искомого частного решения заданного уравнения:

или

15.3 Вопросы для самопроверки.

1. В чём заключается задача разложения функции f(x) в степенной ряд?

2. Как найти интервал сходимости степенного ряда?

3. Как определяются коэффициенты ряда Тейлора?

4. Запишите остаточный член ряда Тейлора.

5. Какой ряд называется рядом Маклорена?

6. В чём состоит метод интегрирования дифференциальных уравнений с помощью степенных рядов?

7. В чём состоит метод интегрирования функции с помощью степенных рядов?

Дата добавления: 2014-12-23