Примеры решения задач. Задача 1. Найти частное решение при начальных

Задача 1. Найти частное решение при начальных

условиях:

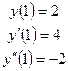
Решение: 1) Проинтегрируем данное уравнение последовательно три раза.

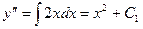(1)

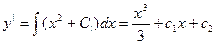(2)

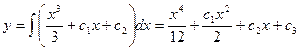(3)- общее решение.

2) Найдём частное решение, подставив соответствующие начальные условия в (1), (2), (3).

(1) 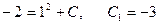(2)

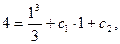
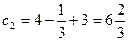
(3) ,

Тогда частное решение имеет вид: ;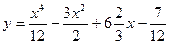

Задача 2. Дано уравнение: (x ² + 1 ) y"= 2 xy'. Найти частное решение, удовлетворяющее начальным условиям: y(0)= 1; y'(0)= 3.

Решение: Данное дифференциальное уравнение второго порядка не содержит явно функцию y. Положим y'=p, где p - некоторая функция аргумента x. Если y'=p, то y"=dp/dx и данное уравнение примет вид 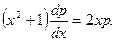Мы получили уравнение первого порядка относительно переменных p и x.

Решим это уравнение: ,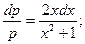

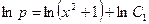откуда или .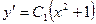

Определим численное значение при указанных начальных условиях. Имеем 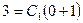. Следовательно, . Теперь решаем уравнение первого порядка y'= 3 (x ² + 1 ):

dy= 3 (x ² + 1 )dx;

.

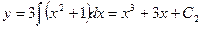Определим численное значение 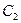при указанных начальных условиях. Имеем ; .

Таким образом, y=x ³ + 3 x+ 1 есть частное решение, удовлетворяющее указанным начальным условиям.

Задача 3. Дано уравнение 2 yy"= (y') ². Найти частное решение,

удовлетворяющее указанным начальным условиям: y (-1) = 4; y' (-1) = 1.

Решение: Данное уравнение второго порядка не содержит явно аргумента x. Положим y'=p, где p -некоторая функция переменной y. Если y'=p, то

Тогда данное уравнение примет вид:

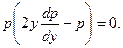
Если приравнять нулю первый множитель, то получаем: p= 0; y'= 0; y=C - решение данного уравнения.

Приравняем нулю второй множитель:

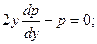
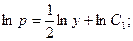
, или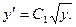

Используя начальные условия, находим : ; .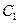

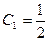Далее решаем уравнение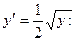

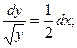
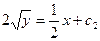
Теперь определим значение :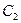

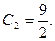
Тогда 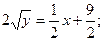и - искомое

частное решение, удовлетворяющее указанным начальным условиям.

Задача 4. Решить систему уравнений и выделить частные решения, удовлетворяющие заданным начальным условиям:

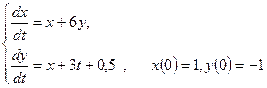
Решение. Обе части первого уравнения системы продифференцируем по переменной t:

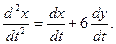
В полученном уравнении заменим правой частью второго уравнения системы. В результате получим неоднородное линейное уравнение второго порядка:

(1)

Составим и решим соответствующее однородное линейное уравнение:

(2)

Характеристическое уравнение k ² -k- 6 =0 имеем корни: . Следовательно, общее решение (2) имеет вид:

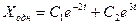
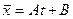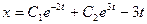Находим частное решение . Дважды дифференцируя, получим . Подставив в (1), находим A= -3 и B= 0. Следовательно, и . (3)

Из первого уравнения системы находим, что или

,

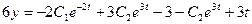откуда 6y=-3C1e^-2t +2C₂^3t+3t-3. (4)

Подставив начальные условия в (3) и (4), получим систему: 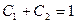и .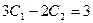

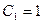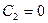Решение этой системы даёт и . Следовательно, 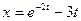и - частные решения, удовлетворяющие заданным начальным условиям.

13.3 Вопросы для самоконтроля.

1. Дайте определение и общего решения этого уравнения. Пример.

2. Изложить план выполнения операции при решении уравнений второго порядка:

а) не содержащих y,

б) не содержащих x.

3. Дать определение линейного дифференциального уравнения 2-го порядка. Привести пример.

4. Как решается 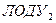с постоянными коэффициентами (описать способ решения).

5. Какой вид имеет общее решение линейного уравнения второго порядка без правой части (с постоянными коэффициентами) 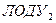в зависимости от корней характеристического уравнения?

6. Разъяснить правило отыскания частного решения линейного уравнения с правой частью f(x)=A·e^mx, f(x)= Pn (x)·e^mx.

7. Какое уравнение называется характеристическим уравнением для линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами?

8. Каков геометрический смысл начальных условий для ?

9. Какова структура общего решения ?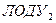

10. Как составляется общее решение для ?

11. Разъяснить правило отыскания частного решения с правой частью f(x)=e^mx(a cos nx+ b sin nx)

12. В чём заключается метод вариации произвольных постоянных?

13. Какая система 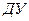называется нормальной?

14. Описать приёмы сведения произвольной системы 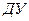к нормальной.

15. Описать приёмы сведения нормальной системы к однородному уравнению высшего порядка.

Дата добавления: 2014-12-23