
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Типы дифференциальных уравнений первого порядка
|
|
|
|
К выполнению контрольной работы №3
Указания
(темы 12-16)
Тема 12. Дифференциальные уравнения 1-го порядка.
Пискунов, гл. VIII, § 1-8, упр. 1-68
Данко, часть II, гл. IV, §1
12.1 Определение дифференциального уравнения первого порядка.
1.Определение. Равенство, связывающее независимую переменную х, функцию у и производные (или дифференциалы) этой функции называются дифференциальным уравнением первого порядка (DY1) т.е.
F (x,y,y')=0 или y'=f (x,y)
Решить дифференциальное уравнение первого порядка – значит, найти неизвестную функцию y.
2. Общим решением дифференциального уравнения первого порядка 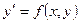 называется функция y= j (x,c), где C - постоянная, которая при подстановке в дифференциальное уравнение первого порядка обращает его в тождество. На плоскости XOY общее решение y=j(x,c) выражает семейство интегральных кривых.
называется функция y= j (x,c), где C - постоянная, которая при подстановке в дифференциальное уравнение первого порядка обращает его в тождество. На плоскости XOY общее решение y=j(x,c) выражает семейство интегральных кривых.
3. Всякое решение y= j (x,С0) полученное из общего решения при конкретном значении С=С0 называется частным решением дифференциального уравнения первого порядка.
4. Задача отыскания частного решения дифференциального уравнения первого порядка 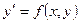 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию
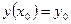 , или
, или 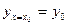 , или
, или
|
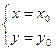
5. 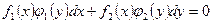 -ДУ1с разделяющимися переменными.
-ДУ1с разделяющимися переменными.
6. 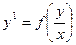 - ОДУ1 – однородное дифференциальное уравнение 1-го порядка или
- ОДУ1 – однородное дифференциальное уравнение 1-го порядка или 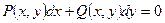 , где
, где 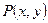 ,
, 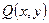 - однородные функции одного измерения. Используется подстановка
- однородные функции одного измерения. Используется подстановка 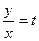
7. 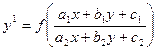 , где
, где 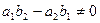 . ДУ1, приводимое к однородному подстановкой
. ДУ1, приводимое к однородному подстановкой
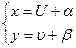 , где
, где 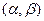 - точка пересечения прямых
- точка пересечения прямых
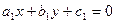 и
и 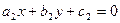
 Если
Если 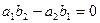 , то используется подстановка
, то используется подстановка 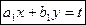
8. 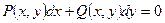 , где
, где 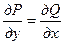 - называется уравнением в полных дифференциалах.
- называется уравнением в полных дифференциалах.
Где 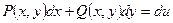 - полный дифференциал функции
- полный дифференциал функции 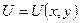
Решить данное уравнение- значит, найти функцию и.
9. 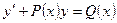 - линейное ДУ1 (ЛДУ1)
- линейное ДУ1 (ЛДУ1)
 Если
Если 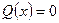 , то уравнение неоднородное,
, то уравнение неоднородное,
Если 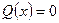 , то уравнение однородное.
, то уравнение однородное.
ЛДУ1 интегрируются:
1) Методом Бернулли (с помощью подстановки y = иv, где u и v -пока неизвестные функции)
2) Методом Лагранжа, варьируя произвольную постоянную.
10. 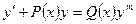 , где m - число, m¹0, m¹1 - дифференциальное уравнение Бернулли, решаемое либо с помощью подстановки y= uv, либо методом Лагранжа (см. пункт 9).
, где m - число, m¹0, m¹1 - дифференциальное уравнение Бернулли, решаемое либо с помощью подстановки y= uv, либо методом Лагранжа (см. пункт 9).
12.2. Примеры решения задач.
Задача 1. Найти частное решение ДУ1 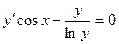 , удовлетворяющему начальному условию
, удовлетворяющему начальному условию 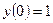 .
.
Решение: Данное уравнение с разделяющимися переменными.
Т.к. 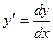 , то уравнение примет вид:
, то уравнение примет вид:
 или
или 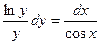 - после отделения переменных.
- после отделения переменных.
Интегрируя обе части последнего уравнения, получим:
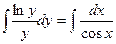 или
или 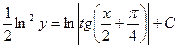 -общее решение
-общее решение
Используя начальное условие 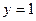 ,
, 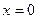 , находим
, находим 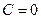 . Тогда из общего решения выделяется частное решение:
. Тогда из общего решения выделяется частное решение:
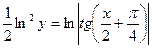
Задача 2. Найти общее решение уравнения 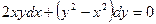
Решение: Данное уравнение является однородным, так как коэффициенты при dx и dy суть однородные функции одного и того же измерения (второго) относительно переменных x и y. Применяем подстановку y=xt, где t - некоторая функция аргумента x. Если y= xt, то дифференциал dy = d(xt) = tdx+ xdt, и данное уравнение примет вид:
2xxtdt+(x²t²-x²) (tdx+xdt)= 0
Сократив на x², будем иметь:
2tdx+(t²-1) (tdx+xdt)=0
2tdx+(t²-1) tdx+x (t²-1)dt=0
t(2+t²-1) dx+x (t²-1)dt=0
t(1+t²)dx= x(1-t²)dt; 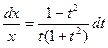 .
.
Мы получили уравнение с разделёнными переменными относительно x и t. Интегрируя, находим общее решение этого уравнения:

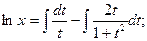
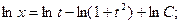
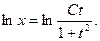
Потенцируя, находим 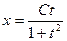 , или x(1+t²)=Ct. Из введённой подстановки следует, что
, или x(1+t²)=Ct. Из введённой подстановки следует, что 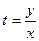 . Следовательно,
. Следовательно, 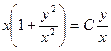 или x²+y²= Cy – общее решение данного уравнения.
или x²+y²= Cy – общее решение данного уравнения.
Задача 3. Найти общее решение уравнения y'-y tg x=2 xsec x.
Решение: Данное уравнение является линейным, так как оно содержит искомую функцию y и её производную y' в первой степени и не содержит их произведений.
Применяем подстановку y= uv, где u и v –некоторые неизвестные функции аргумента x. Если y=uv, то y'= (uv)'= u'v+uv' и данное уравнение примет вид: u'v+uv'-uvtg x= 2x sec x,
или
v(u'-utg x)+ uv'= 2xsec x. (1)
Так как искомая функция y представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию u так, чтобы выражение, стоящее в круглых скобках левой части неравенства (1), обращалось в нуль, т.е выберем функцию u так, чтобы имело место равенство
u'-utg x= 0 (2)
При таком выборе функции u уравнение (1) примет вид
uv'= 2 x sec x. (3)
Уравнение (2) есть уравнение с разделяющимися переменными относительно u и x. Решим это уравнение:
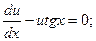
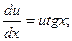
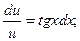
 ln u= -ln cos x,
ln u= -ln cos x, 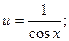 или
или 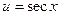
(Чтобы равенство (2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной C=0.) Подставив в (3) найденное выражение для u, получим:
secxv'= 2 xsecx; v'= 2 x; 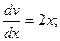 dv= 2 xdx. Интегрируя, получаем v=x²+C. Тогда y=secx(x²+C) - общее решение данного уравнения.
dv= 2 xdx. Интегрируя, получаем v=x²+C. Тогда y=secx(x²+C) - общее решение данного уравнения.
12.3. Вопросы для самоконтроля.
1. Какое уравнение называется дифференциальным?
2. Как определяется порядок уравнения? Примеры.
3. Что значит решить  ?
?
4. Какая функция называется решением 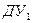 ?
?
5. Какое решение называется общим, частным?
6. Как найти частное решение 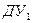 по начальным условиям? Записать план операций, выполняемых при решении на примере y'- 2 x= 0 при начальных условиях y (-2) = 4.
по начальным условиям? Записать план операций, выполняемых при решении на примере y'- 2 x= 0 при начальных условиях y (-2) = 4.
7. Сформулировать геометрический смысл общего и частного решения 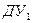 .
.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1140; Нарушение авторских прав?; Мы поможем в написании вашей работы!