Теория предела

Эпилог.

Во двор большого двухэтажного коттеджа въехал черный ровер. Из него вышел Ратэк и, от крыв заднюю дверцу, вытащил из машины переносную люльку с ребенком. Митя, которому шел уже шестой месяц, даже не проснулся, сладко посапывая, уставший после прогулки с отцом. Маритту немного пугал энтузиазм, с которым подходил Дарн к вопросу общения с ребенком. Никакие уговоры и объяснения девушки о том, что ребенок еще слишком мал и ему рановато посещать зоопарки, океанариумы и парки с каруселями на Мирэка не действовали. Он говорил, что Митя так будет быстрее развиваться, и, как следствие, умнеть. "Похоже", - бурчала Ита, - "он собирается вырастить супер ребенка. Эрудита, спортсмена и так далее по списку". В конце концов, она махнула рукой: ну чем ребенку может повредить осмотр всяких там тюленей и жирафиков. А уж на то, как грозный Ратэк втискивается в вагончик детского поезда, чтобы повозить на коленях ребенка, Ита без смеха смотреть не могла. Она так ухохатывалась, икая и держась за живот, что Дарнов даже обиделся.

Передав переноску с сыном Антону, Мирэк улыбнулся Ите:

- Ну, как, отдохнула?

Девушка пожала плечами. После общения с Дарновым у нее на сердце оставалась какая-то тихая грусть с привкусом горечи. Этого она объяснить себе не могла. И поэтому ощущала себя неудобно.

Тоха понес ребенка в дом по пути окликая Надежду. Дарн приобнял Маритту за талию и наклонился к ее уху:

- Я умею ждать, милая. И думаю, ты очень скоро передумаешь.

Ита отчаянно замотала головой.

- Ты просто еще очень плохо знаешь Шторма. Он неплохой мужик, но..., - Ратэк криво усмехнулся, чмокнул ее в висок и быстрым шагом пошел к машине, а Ита осталась стоять на крыльце растерянно хлопая ресницами.

Мирэк уже выезжал со двора, когда к девушке присоединился Антон.

- Чего он тебе сказал? - нахмурился он.

- Ничего такого, чего бы я хотела от него услышать, - беспечно отозвалась Ита.

- А что бы ты хотела от него услышать? - Тоха ревниво прищурился.

- Ну, например, что есть такого ценного в этих землях Дарнова, что за ними все так охотились? Что-то я сильно сомневаюсь, что Алонзо планировал заняться сельскохозяйственной деятельностью...

Шторм ухмыльнулся и, взяв ее за руку, повел в дом.

- Ты знаешь? Знаешь? - теребила его Маритта.

Антон повернулся к ней, с усмешкой покачал головой так, что девушка не поняла "да" это или "нет". Он подхватил ее на руки и понес в спальню.

Смысл предела (конечного) функции в точке .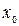

В основу формирования понятия предела рекомендуем положить наглядное представление о нем. В этом случае изложение нового материала можно проводить следующим образом.

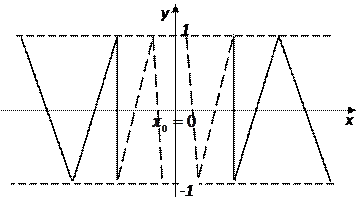
Рассмотрим графики функций, изображенных на рис. 2. Если интересоваться поведением функции вблизи точки 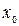, то функция с графиком рис.2.1 обладает важным свойством, отличающим ее от остальных, а именно:

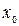а) Функция вблизи точки ведет себя «спокойно» в том смысле, что существует число (см. рис. 2, где оно «представлено» прямой ) такое, что для всех значений из малой окрестности 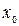, лежащих и справа и слева от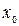

и тем точнее, чем меньше берется окрестность.

Это свойство можно выразить и другими словами;

    Рис. 2.1 Рис. 2.2

б) При приближении к 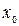(), но не обязательно , и справа и слева значения функции приближаются к одному и тому же числу ().

Рис.2.3 Рис.2.4

Рис. 2

Этим свойством не обладают остальные функции на рис. 2. Так, значения функции при стремлении к 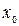справа () приближаются к числу , а при слева к числу (см. рис. 2.2)). Функция в любой окрестности точки успевает принять все значения от -1 до 1.

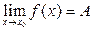Свойство функции, описанное в высказываниях а), б) и рисунком 2.1, выражает сущность предела функции в точке . Именно в этом случае говорят, что число является пределом функции при и обозначают или .

Определение предела функции в точке .

Описательный характер вышеприведенных высказываний не дает возможности «работать» с новым понятием (вычислять пределы, строго доказывать свойства, теоремы и т.п.). Поэтому приходится вводить более громоздкий аналитический язык «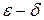», использующий арифметические операции, модуль, неравенства и др.

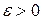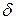Зададим погрешность . Поскольку по смыслу предела вблизи , то найдется такая - окрестность точки , в которой является приближенным значением с точностью , т.е. . Таким образом, мы пришли к следующему определению:

Определение 1. Число называется пределом функции при , стремящемся к , если для любого числа 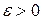найдется такое число , что для всех , удовлетворяющих неравенству 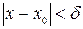, выполняется неравенство . Или более коротко: число есть предел функции при , если для любого 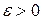найдется такое , что

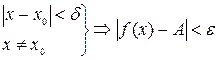(1)

Для выяснения геометрического смысла предела неравенства слева и справа в формуле (1) запишем в виде равносильных двойных неравенств

(2)

и на координатной плоскости проведем горизонтальные прямые , , и вертикальные , , (рис.3).

Рис.3

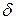Определение предела приобретает следующий геометрический смысл: Число есть предел функции при , если для любой полосы (сколь угодно малой ширины) шириной (между линиями и ) найдется такая - окрестность точки , что часть графика функции, заключенная между вертикальными линиями и , лежит в этой полосе (за исключением, может быть ) (см. рис.3).

Обратим внимание на условие «» в определении. Оно говорит, что значение функции в точке никакой роли не играет. Функция может в этой точке быть вообще не определена или принимать любое значение. Ни на существование предела, ни на его значение это не влияет.

В теории пределов значение функции в точке не рассматривается.

Все функции на рис.4 имеют предел в точке . Это объясняется тем, что понятие предела возникло при введении другого фундаментального понятия математике – производной. А там рассматриваются пределы вида , для которых функция в самой точке не определена (знаменатель обращает в нуль).

Замечание: определение предела сформулировано так, что его можно рассматривать лишь в таких точках , некоторая окрестность которых целиком принадлежит области определения функции.

Строго следуя такому определению, мы не можем говорить о пределе функции 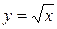в точке , так как она определена лишь справа от 0.

Возвращаясь к смыслу предела, рекомендуем далее рассматривать один из видов рассуждений, использующих новое понятие. Пусть известно существование предела 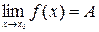и какая-то информация о числе . Так как по смыслу предела вблизи , то тем же свойством, что и должны обладать и значения функции хотя бы в малой окрестности .

Можно рассмотреть несколько задач такого вида. Решения этих задач не требуют никаких вычислений и легко просматриваются на рисунке. Задачи выражают общие и важные свойства функций, имеющих предел, поэтому их можно назвать свойствами. Первое из них находит важное применение в дифференциальном исчислении.

Свойство 1.1 Пусть 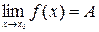и . Тогда существует такая 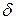- окрестность точки 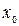, в которой (за исключением может быть ) , т.е.

Доказательство. Выберем 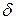- полосу так, чтобы прямая была ее нижней границей (см. рис.8) (для этого нужно взять , и тогда 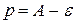). На основании определения предела найдется такая 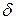- окрестность точки 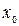, для которой график функции (за исключением может быть ) лежит в построенной полосе и, следовательно, выше прямой , что и означает .

  Рис. 8 Рис. 9

Рис. 8 Рис. 9

Столь же проста и аналитическая запись доказательства. Она считывается с рис.8. Возьмем . Тогда 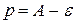. Для этого на основании определения предела найдем такое, что

Здесь мы использовали формулы (1) и (2).

Аналогично доказывается и свойство 1.2.

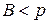Свойство 1.2 Пусть и . Тогда существует такая 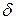- окрестность точки 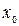, в которой (за исключением может быть ) .

В качестве упражнений повышенной трудности можно рассмотреть свойства 2 и 3.

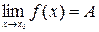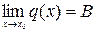Свойство 2. Пусть и и 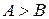, то существует 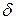- окрестность точки 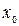, в которой (за исключением, быть может, ) (см. рис.9).

Свойство 3. Если существует 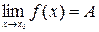, от для любого найдется 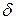- окрестность точки 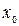, в которой

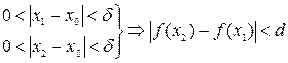(см. рис. 10)

Рис. 10

Дата добавления: 2015-03-29