
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характер разрыва монотонной функции
|
|
|
|
Теорема: Пусть на [a;b] задана не убывающая функция y = f(x). Тогда в любой 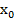 - данного отрезка функция f(x) либо непрерывна либо имеет разрыв первого рода.
- данного отрезка функция f(x) либо непрерывна либо имеет разрыв первого рода.
Доказательство
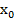 ∊ (a;b)
∊ (a;b)

Рассмотрим в 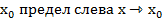 -0, при этом все последовательности, ограничены сверху f(x)≤f(
-0, при этом все последовательности, ограничены сверху f(x)≤f(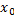 )
)
lim f(x)<f(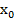 )
)
x 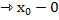
Последовательность сходящаяся справа: x⇾ 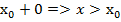
f(x)≥f(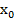 )
)
lim f(x)≥f(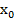 )
)
x 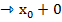
f(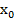 - 0)≤f(
- 0)≤f(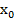 )≤f(
)≤f(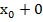 )
)
f(a) ≤ f(a+0)
f (b) ≥ f (b-a)
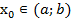
Таким образом, теорема доказана.
Теорема: Для того чтобы монотонная функция на [a;b] была непрерывна, необходимо и достаточно, чтобы она принимала все промежуточные значения между f(a) и f(b).
Лемма 1: Если непрерывная на отрезке [a;b] функция y = f(x) на концах отрезка принимает значения разных знаков, то ∃℥ ∊ [a;b], в которой f(℥) = 0
f∊C[a;b] – f непрерывна на [a;b]
f(a)·f(b)<0 => ∃℥∊[a;b]: f(℥) = 0
Лемма 2: Если f(x) непрерывна в 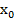 и f(
и f(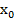 ) ≠ 0, то в некоторой окрестности
) ≠ 0, то в некоторой окрестности 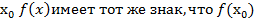
Доказательство
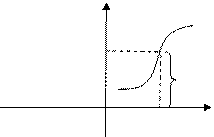 ∀ε>0 ∃𝛿>0 ∀x∊(
∀ε>0 ∃𝛿>0 ∀x∊(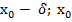 +𝛿) y
+𝛿) y
ε = 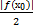
|f(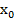 ) – f(
) – f(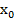 )|<ε f(
)|<ε f(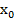 )
)
f(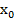 ) – ε < f(x) < f(
) – ε < f(x) < f(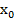 ) + ε 2ε
) + ε 2ε
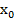 x
x
Что и требовалось доказать.
Теорема: Если y = f(x) непрерывна и монотонна на [a;b], то она имеет обратную, которая также монотонная и непрерывная на отрезке [f(a); f(b)] или [f(b); f(a)]
Следствие всех теорем, а также и пределов сложных функций является непрерывность всех элементарных функций на своей области определения.
Ограниченность. Существование наибольшего и наименьшего значений функции, непрерывных на отрезке (компакте)
Теорема: Пусть y = f(x)- непрерывна на [a;b], то она ограничена на этом отрезке, т.е. существует такое n>0, что |f(x)|<M ∀x∊[a;b]
f(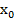 ) - ε≤f(x)≤f(
) - ε≤f(x)≤f(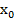 ) + ε
) + ε
x ∊ (ε + 𝛿; 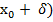

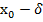
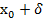
а 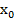 b
b
Пусть 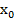 - любая.
- любая.
По т. Гейне Бореля существует конечное покрытие отрезка [a;b].
|
|
|
(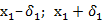 )
)
(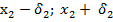 )
)
…
(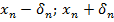 )
)
f(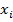 ) -
) - 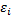 ≤ f(x) ≤ f(
≤ f(x) ≤ f(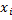 ) +
) + 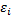
1 ≤ i ≤ n
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 505; Нарушение авторских прав?; Мы поможем в написании вашей работы!