Основные свойства передаточных функций

Понятие передаточной функции лежит в основе классической теории автоматического регулирования. В связи с этим ниже перечисляются основные её свойства, используемые при анализе систем автоматического управления.

1. Элемент 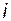-й строки и 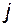-го столбца матричной передаточной функции равен отношению изображения 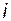-й координаты вектора выхода к 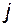-й координате вектора управления при нулевых начальных условиях:

. (2.6.11)

Таким образом,

. (2.6.12)

2. Для стационарных объектов с сосредоточенными параметрами элементы матричной передаточной функции - это дробно-рациональные функции комплексной переменной :

(2.6.13)

3. По известной передаточной функции легко восстанавливаются соответствующие дифференциальные уравнения. По данным предыду­щего примера

.

После приведения к общему знаменателю получаем

,

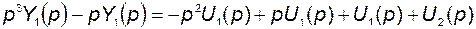и в результате имеем

.

4. Знаменатель передаточной функции - это соответствующий харак­те­ри­стический полином. Полюсы передаточной функции - это корни соответ­ству­ющего характеристического полинома.

5. Поскольку весовая функция является оригиналом для передаточной, то при всех различных полюсах

, (2.6.14)

где 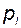- полюсы функции;

; (2.6.15)

- коэффициенты при старших степенях 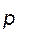числителя и знаменателя передаточной функции ;

- нули .

6. В физически реализуемых системах порядок числителя 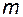элементарной передаточной функции не может превышать порядка ее знаменателя .

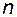7. В простейших случаях элементарная передаточная функция может быть непосредственно получена из соответствующего дифференци­аль­но­го уравнения. Например, для динамического звена с уравнением

путем перехода к изображениям по Лапласу при нулевых начальных условиях получаем

,

откуда

.

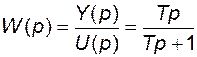При описании пассивных электрических цепей передаточные функции могут вычисляться в соответствии с правилами электротехники с использованием полных символических сопротивлений. Так, например, для схемы, приведенной на рис.2.17,

.

8. Если существует предел переходной функции при стремлении времени к бесконечности, то

.

Кроме того, справедливо равенство

.

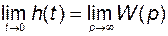Эти формулы следуют из предельных теорем преобразования Лапласа:

и .

Дата добавления: 2015-03-31