Типовые соединения многомерных линейных систем

Структурные схемы и графы стационарных систем

Одной из характерных задач анализа САУ является задача преобразования и упрощения исходных структурных схем. При этом используются правила преобразования простейших, типовых соеди­не­ний, к которым относят параллельное (согласно-параллельное) (рис 2.25), последовательное (рис 2.26) и встречно-параллельное, когда одно динамическое звено включено в обратную связь другому (рис 2.27). Для каждой из этих ситуаций нетрудно найти передаточную функцию эквивалентного звена.

Пусть исходные динамические звенья имеют следующее описание:

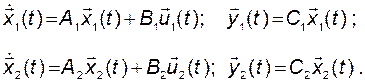(2.8.1)

Параллельное соединение (рис. 2.25)

В случае параллельного соединения звеньев введем в рассмот­ре­ние следующие очевидные равенства из блочных векторов и матриц:

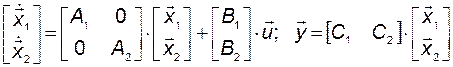. (2.8.2)

В соответствии с этим можно записать выражение для эквивалентной

передаточной функции соединения

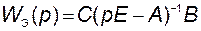, (2.8.3)

где

. (2.8.4)

Учитывая, что

,

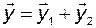а

,

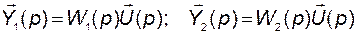получаем

. (2.8.5)

С другой стороны, передаточную функцию эквивалентного звена можно расписать следующим образом:

,

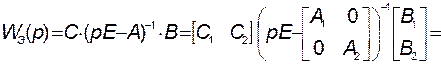
где – размерности соответствующих единичных матриц.

Продолжим преобразования:

.

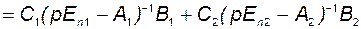Таким образом, в результате получаем

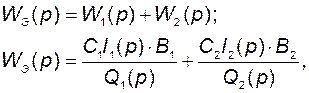(2.8.6)

где

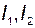– соответствующие присоединенные матрицы для матриц 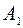и ;

- характеристические полиномы первого и второго звеньев, то есть

;

.

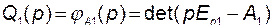Характеристический полином эквивалентной системы (матрицы ) имеет вид

. (2.8.7)

Отсюда следует, что нули характеристического полинома (полюсы) эквивалентной передаточной функции соединения состоят из нулей характеристических полиномов (полюсов передаточных функций) первого и второго звеньев.

Таким образом, если каждое из параллельных звеньев устойчиво, то и всё соединение в целом устойчиво; если в соединении присутствует хотя бы одно неустойчивое звено, то соединение в целом неустойчиво (связь между характером полюсов передаточной функции и устойчивостью соответствующей системы будет обсуждаться в п. 2.9).

Последовательное соединение (рис. 2.26)

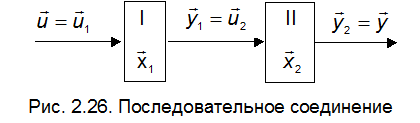
При последовательном соединении блочные уравнения имеют вид

, (2.8.8)

и в выражении (2.8.3) для эквивалентной функции

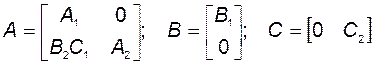. (2.8.9)

Кроме того, нетрудно получить связь между передаточными функциями отдельных звеньев, входящих в соединение, и эквивалентной передаточ­ной функцией

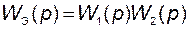. (2.8.10)

Вывод о связи между устойчивостью отдельных звеньев и устойчивостью их последовательного соединения аналогичен выводу для случая параллельного включения.

Встречно-параллельное включение звеньев рис. 2.27

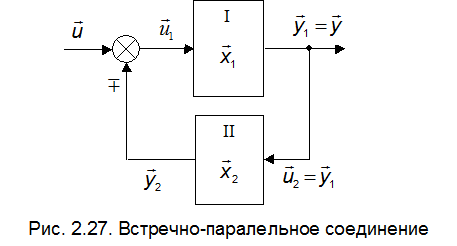
Для встречно-параллельного соединения, учитывая, что , получаем

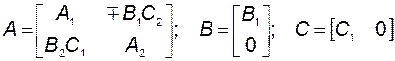(2.8.11)

и

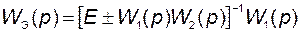. (2.8.12)

Поскольку полюсы передаточной функции эквивалентного соединения в данном случае не удается выразить непосредственно через полюсы передаточных функций отдельных звеньев, то однозначного ответа об устойчивости соединения без дополнительного анализа получить не удается.

Дата добавления: 2015-03-31