Графы динамических систем

Графом называется множество вершин и ребер, в котором каждому ребру соответствует две вершины - начало и конец ребра.

Основные характеристики графов:

1) каждой вершине на графе, изображаемой кружком или точкой, ставится в соответствие величина одной из переменных (координат системы);

2) каждое ребро, изображаемое на графе линией со стрелкой, имеет вершину –“начало” и вершину – “конец”. Стрелка обозначает направление передачи сигнала от начала к концу, таким образом, граф прохождения сигналов является направленным (антисимметричным) графом;

3) величина, соответствующая началу (вершине) ребра, называется входной величиной ребра. Если из вершины выходит несколько ребер, то входные величины этих ребер одинаковы и равны величине соответствующей вершины;

4) ребро изображает одно из звеньев в системе и ему ставится в соответствие передаточная функция;

5) если к вершине подходит несколько ребер, то сопоставляемая ей величина равна сумме выходных величин ребер.

Между графом прохождения сигналов и структурной схемой имеется взаимно однозначное соответствие. Стрелка структурной схемы соответствует вершине графа, а прямоугольник (звено) – ребру. При необходимости в граф системы могут вводиться дополнительные единичные ребра для выявления промежуточных координат, являющихся, как правило, выходами отдельных ребер. Для примера приведены графические представления некоторой системы в виде структурной схемы (рис. 2.28) и графа (рис. 2.29).

Простейшие правила преобразования структурных схем и графов линейных систем представлены в таблице.

№п/п	Структурная схема	Граф	Эквивалентная передаточная функция
	Параллельное соединение звеньев
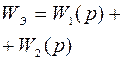
	Последовательное соединение звеньев
	Встречно-параллельное соединение звеньев

Встречаются и более сложные случаи соединения звеньев, так, например, соединения с перекрестными связями (рис. 2.30).

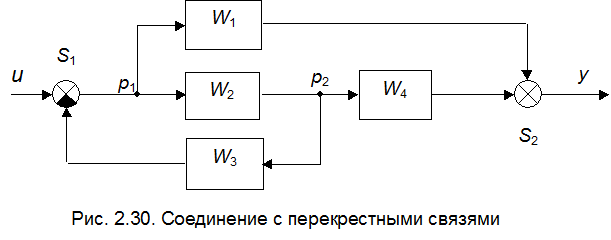
В этих случаях можно пользоваться правилом переноса динамического звена через сумматор или точку разветвления.

Любое динамическое звено можно перенести через сумматор или точку разветвления; при этом звено должно войти во все входящие и ответвляющиеся ветви. В те ветви, в которые звено входит без изменения направления распространения сигнала, звено проходит со своей передаточной функцией. В тех ветвях, при продвижении в которые меняется направление распространения сигнала, передаточная функция звена изменяется на обратную.

Это правило иллюстрируется элементарными примерами, приведёнными на рис. 2.31 – 2.34.

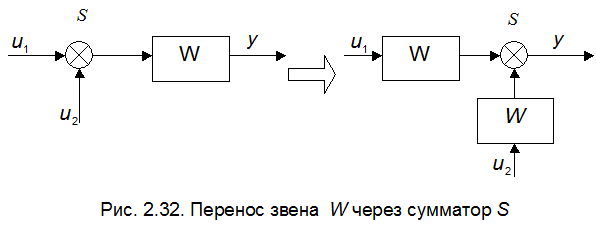
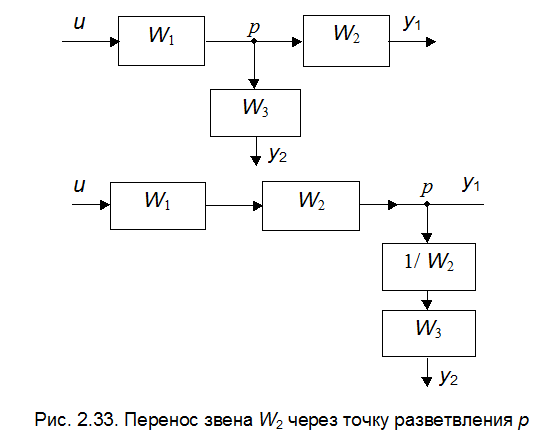
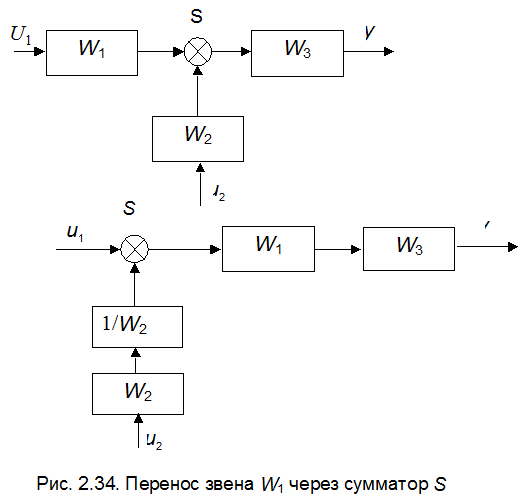
В качестве примера проведём упрощение структурной схемы, приведённой на рис. 2.30. Перенесём динамическое звено с передаточной функцией 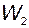через точку разветвления . После этого получим схему, состоящую только из элементарных соединений (рис. 2.35).

Теперь исходная система может быть представлена в упрощенном виде (рис 2.36) и будет описываться выражением .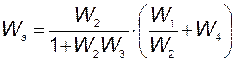

Дата добавления: 2015-03-31