Асимптотические свойства собственного движения и весовой матрицы линейной системы

Устойчивость систем

Пусть нелинейное дифференциальное уравнение состояния имеет вид

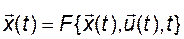. (2.9.1)

Пусть также – некоторая заданная (номинальная) функция времени и – некоторый номинальный вектор начальных условий.

Решение 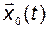является устойчивым в смысле Ляпунова, если для любого и для любого существует 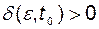такое, что при

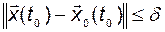(2.9.2)

удовлетворяется неравенство

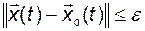. (2.9.3)

Норма вектора 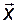в простейшем случае совпадает с его евклидовой длиной

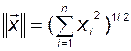. (2.9.4)

Возможно также использование и других форм нормы, например

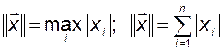. (2.9.5)

Введение нормы в пространстве состояний дает возможность ввести понятие близости точек пространства. Устойчивость в смысле Ляпунова гарантирует, что состояние 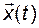не отклоняется далеко от «номинального» режима 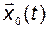при начальном состоянии 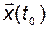, достаточно близком к номинальному начальному состоянию .

Решение 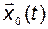называется асимптотически устойчивым, если оно устойчиво в смысле Ляпунова, и для любого 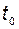существует такое 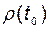, что при

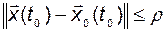(2.9.6)

выполняется условие

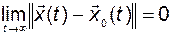. (2.9.7)

Решение 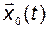является асимптотически устойчивым в целом, если оно устойчиво по Ляпунову, и для любых и

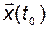
. (2.9.8)

Применительно к нелинейным системам, вследствие сложности харак­терных для них явлений, обсуждается обычно устойчивость решений. В линейных системах ситуация проще, и в этом случае целесообразнее говорить об устойчивости уже не решения, а самой системы. Пусть дано уравнение системы

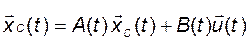, (2.9.9)

и для , 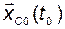и при 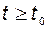известно 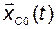, то есть справедливо уравнение

. (2.9.10)

Естественно, что при других начальных условиях решение будет другим

. (2.9.11)

Вычтем из (2.9.11) уравнение (2.9.10):

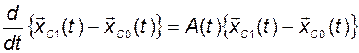(2.9.12)

Обозначив

,

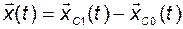при начальных условиях

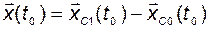
получим уравнение

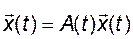, при . (2.9.13)

Таким образом, понятие устойчивости решения можно свести к поня­тию устойчивости линейной системы.

Линейная система устойчива в определенном смысле (по Ляпунову, асимптотически или асимптотически в целом), если тривиальное решение 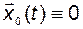устойчиво в этом смысле.

Линейная система асимптотически устойчива тогда и только тогда, когда она асимптотически устойчива в целом.

Таким образом, исследование вопроса устойчивости решений линейной неавтономной системы сводится к исследованию решения соответствующего однородного дифференциального уравнения, которое определяется матрицей и имеет вид

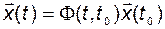; (2.9.14)

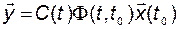. (2.9.15)

Рассмотрим три возможных случая.

1. 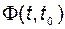– ограниченная матрица в интервале , то есть существует такое положительное числ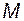о , что

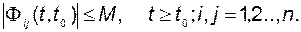
Тогда получаем, что

,

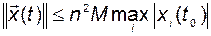и условие устойчивости выполняется, если взять, например,

.

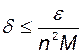2. Переходная матрица удовлетворяет условию

.

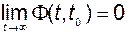При этом движение, а значит, и сама система являются асимптотически устойчивыми.

3. 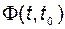– неограниченная матрица в интервале . При этом движение неустойчиво, так как для любого

.

Это означает и неустойчивость самой системы.

Если система является наблюдаемой и управляемой (эти понятия будут рассмотрены в пп. 3.2, 3.3), то устойчивость системы можно исследовать с помощью весовой функции. Система асимптотически устойчива, если

.

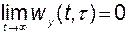Итак, линейная система является асимптотически устойчивой, если ее переходная матрица с течением времени стремится к нулевой матрице. Для стационарных систем, то есть для систем с постоянными параметрами, это условие эквивалентно требованию, чтобы все собственные числа матрицы имели отрицательные действительные части, то есть лежали в левой полуплоскости плоскости комплексной переменной 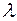. Это следует из формы представления переходной матрицы через собственные числа и правые и левые собственные векторы матрицы в соответствии с (2.4.28). Таким образом, анализ устойчивости системы может быть сведен к анализу расположения собственных чисел матрицы , или, что то же самое, расположения полюсов передаточной функции полностью управляемой и наблюдаемой системы.

В теории автоматического управления разработан ряд методов, называемых критериями устойчивости, позволяющих проанализировать расположение собственных чисел относительно мнимой оси плоскости 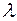и не требующих при этом точного решения соответствующего характеристического уравнения. К первой группе этих методов относятся так называемые алгебраические критерии, которые путем элементарных вычислений по коэффициентам характеристического полинома позволяют проанализировать устойчивость исследуемой системы с известными значениями ее параметров.

Дата добавления: 2015-03-31