КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Мейсона
|
|
|
|
В случае громоздких систем с большим числом звеньев и перекрестных связей наиболее эффективным является использование для получения эквивалентных передаточных функций правила Мейсона. В связи с этим введем необходимые дополнительные определения.
Прямой путь между двумя заданными вершинами графа – это непрерывная последовательность ветвей одного направления, в которой каждая из вершин встречается не более одного раза.
Контур – замкнутая цепь, при однократном обходе которой в направлении, указанном стрелками, каждая из вершин встречается не более одного раза.
Согласно правилу Мейсона, передаточная функция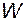 
между входом в точке 
и выходом в точке 
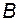равна
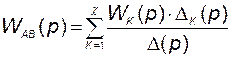, (2.8.13)
где
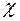– число прямых путей между вершинами и ;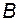
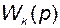– передаточная функция k-го прямого пути от вершины к вершине 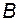(она равна произведению передаточных функций всех ребер, входящих в последовательность прямого пути);
– определитель графа;
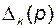– k-й минор определителя графа, равный определителю более простого графа, который получается из данного графа путем удаления из него всех ребер и вершин, лежащих на k-м прямом пути, а также всех ребер, входящих в эти вершины и исходящих из этих вершин.
Определитель графа определяется из соотношения
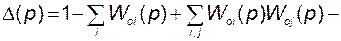
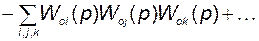, (2.8.14)
где
– передаточные функции различных контуров графа;
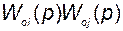– произведения передаточных функций непересекающихся пар контуров;
– произведения передаточных функций непересекающихся троек контуров.
ПРИМЕР 2.8.1. Найти передаточную функцию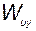 
для системы, структурная схема которой приведена на рис. 2.37.
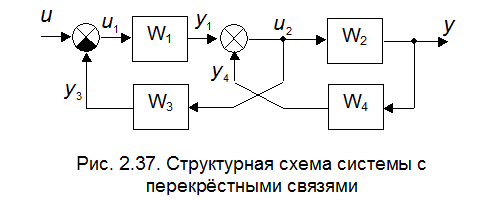
Этой схеме соответствует граф, представленный на рис. 2.38.
Для этого графа:
§ передаточная функция единственного прямого пути
|
|
|
;
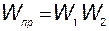§ передаточные функции контуров
; 
;
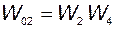§ главный определитель
; 
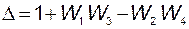§ определитель прямого пути
;
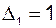§ искомая передаточная функция
.
ПРИМЕР 2.8.2. Найти передаточную функцию между точками и 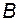для графа, приведённого на рис. 2.39.
§ Передаточные функции прямых путей:
W1=Wa·Wb·Wc;
W2=Wa·Wd·We·Wc;
W3=Wa·Wd·Wg·Wh.
§ Передаточные функции контуров:
W01= Wd·Wg·Wh·Wn·Wr·Wp·Wl;
W02= Wd·We·Wc·Wn·Wr·Wp·Wl;
W03= Wb·Wc·Wn·Wr·Wp·Wl;
W04= Wc·Wn·Wr·Wm;
W05= Wr·Wp·Wq;
W06=Wg Ws;
W07= Wg·Wf.
§ Произведения передаточных функций непересекающихся пар контуров:
W02·W07; W03·W06; W03·W07; W04·W06; W04·W07; W05·W06; W05·W07.
§ Непересекающихся троек контуров нет.
§ Определитель графа:
Δ=1- W01 - W02 - W03 - W04 - W05 - W06 - W07+
+ W02·W07+W03·W06+W03·W07+W04·W06+W04·W07+W05·W06+W05·W07.
§ Миноры определителя графа:
Δ1=1-W05-W07-W06+W05·W06+W05·W07;
Δ2=1-W05-W07+W05·W07;
Δ3=1-W05.
§ Результирующая передаточная функция
.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 10097; Нарушение авторских прав?; Мы поможем в написании вашей работы!