Критерий Гурвица

Критерий устойчивости Гурвица

Пусть характеристический полином некоторой системы имеет вид (2.9.16). Сопоставим этому полиному матрицу Гурвица:

. (2.9.18)

По главной диагонали стоят коэффициенты полинома, остальные элементы строятся по следующему принципу: вверх от диагонального элемента ставятся коэффициенты полинома в порядке возрастания индексов, вниз - коэффициенты полинома в порядке убывания индексов. Элементы, требующие индексов, больших степени полинома или отрицательных, устанавливаются нулевыми.

Для устойчивости системы необходимо и достаточно, чтобы при а₀>0 были положительны все (n) главные миноры матрицы Гурвица.

Рассмотрим примеры конкретизации критерия Гурвица для простейших случаев.

§

Запишем дифференциальное уравнение

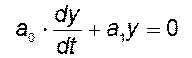
и характеристическое уравнение

.

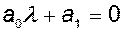В данном случае применение критерия Гурвица даёт тривиальный результат:

.

§

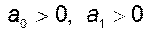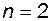
Запишем дифференциальное уравнение

,

характеристическое уравнение

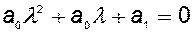
и матрицу Гурвица

.

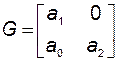Как и в предыдущем случае, при применение критерия Гурвица даёт тривиальный результат:

.

Отметим, что для систем первого и второго порядка необходимое условие устойчивости является и достаточным.

§

Запишем характеристическое уравнение

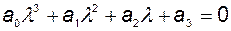
и матрицу Гурвица

.

Для устойчивости системы по критерию Гурвица необходимо и достаточно, чтобы при 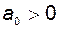были положительны первый

,

второй

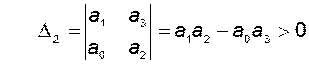
и третий

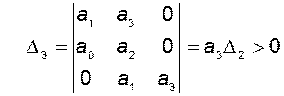
главные миноры матрицы Гурвица. С учётом необходимого условия устойчивости (требования положительности всех коэффициентов характеристического уравнения) критерий Гурвица для устойчивости системы третьего порядка требует выполнения неравенства

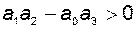. (2.9.19)

§

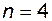
Запишем характеристическое уравнение

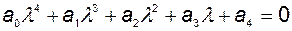
и матрицу Гурвица

.

Для устойчивости системы по критерию Гурвица необходимо и достаточно, чтобы при 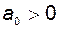были положительны первый

,

второй

,

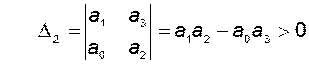третий

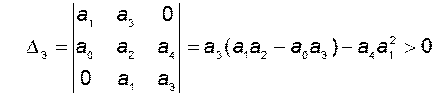
и четвёртый

главные миноры матрицы Гурвица. С учётом необходимого условия устойчивости (требования положительности всех коэффициентов характеристического уравнения) критерий Гурвица для устойчивости системы четвёртого порядка требует выполнения неравенства

. (2.9.20)

Для системы пятого порядка критерий Гурвица выливается в требование выполнения уже двух неравенств:

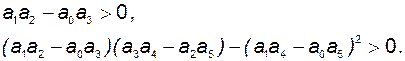(2.9.21)

С дальнейшим увеличением порядка систем использование критерия Гурвица становится всё более громоздким и теряет смысл. Если возникает необходимость привлечения вычислительной техники, то в наше время проще непосредственно вычислить корни характеристического уравнения. Тем не менее, для систем третьего - четвёртого порядков привлекает простота использования критерия Гурвица.

ПРИМЕР 2.9.1. Рассмотрим систему, представленную на рис. 2.40, с входным сигналом 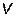, сигналом ошибки и выходным сигналом .

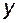Этой системе соответствует передаточная функция

.

В соответствии со свойствами передаточных функций характеристический полином замкнутой системы имеет вид

.

По критерию Гурвица система устойчива, если выполняется неравенство

.

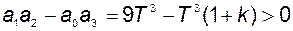Отсюда, с учётом требования положительности всех коэффициентов характеристического полинома, следует, что система устойчива, если при выполняются неравенства

.

Значения параметров, при которых система находится на границе устойчивости, принято называть критическими. В данном примере у коэффициента имеется два критических значения - нижнее и верхнее .

Дата добавления: 2015-03-31