Анализ устойчивости замкнутой системы

Принцип приращения аргумента

Обозначим

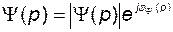, (2.9.28)

тогда

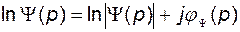. (2.9.29)

С учётом (2.9.27) получаем:

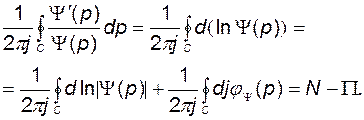(2.9.30)

Поскольку в правой части равенства стоит вещественное число, то мнимая часть левой части равенства также равна нулю.

Таким образом, если функция 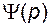аналитична в замкнутой области 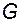, ограниченной контуром , за исключением конечного числа полюсов в области 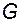, и если функция 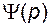не имеет ни полюсов, ни нулей на контуре , то приращение аргумента функции 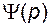при движении вектора по замкнутому контуру определяется выражением

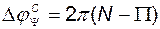. (2.9.31)

Рассмотрим замкнутую систему с единичной обратной связью (рис. 2.41). Пусть известно, что среди 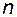полюсов 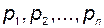передаточной функции разомкнутой системы

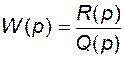(2.9.32)

имеется 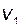нулевых и 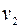чисто мнимых полюсов на верхней полуплоскости плоскости комплексной переменной (рис 2.42), то есть

. (2.9.33)

Образуем функцию

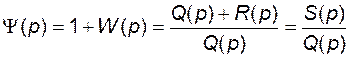, (2.9.34)

характерную тем, что ее знаменатель является характеристическим полиномом разомкнутой системы, а числитель – характеристическим полиномом замкнутой.

Выберем в качестве области 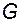всю правую полуплоскость плоскости комплексной переменной . Контур сформируем из мнимой оси, за исключением точек, совпадающих с полюсами передаточной функции разомкнутой системы, дуг окружностей бесконечно малого радиуса, охватывающих эти полюсы, как показано на рис. 2.42, и окружности бесконечно большого радиуса, охватывающей всю правую полуплоскость.

Допустим, в общем случае, что разомкнутая система неустойчива и её передаточная функция имеет 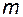"неустойчивых" полюсов, то есть 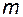полюсов в правой полуплоскости плоскости комплексной переменной . Предположим, что замкнутая система также неустойчива и 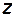– число неустойчивых полюсов передаточной функции замкнутой системы. Тогда, в соответствии с принципом приращения аргумента,

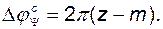(2.9.35)

Если обходить контур в отрицательном направлении, совпадающем с положительным направлением мнимой оси, то

. (2.9.36)

Будем сопоставлять изменение комплексной переменной р при перемещении ее вдоль контура на плоскости и соответствующее ему изменение функции 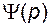на комплексной плоскости 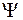. Для этого разобьем контур на несколько характерных участков.

На участке I годограф комплексной переменной изменяется по окружности бесконечно большого радиуса, охватывая всю правую полуплоскость, то есть

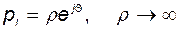. (2.9.37)

Ранее отмечалось, что в физически реализуемых системах порядок числителя передаточной функции не может превышать порядок ее знаменателя. Отсюда следует, что степени полиномов и 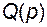равны, а значит,

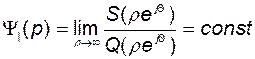. (2.9.38)

Таким образом, приращение фазы функции 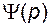при изменении вдоль первого участка равно нулю:

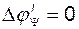. (2.9.39)

В качестве участка II выберем мнимую ось плоскости , то есть

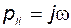, (2.9.40)

за исключением тех ее точек, в которых располагаются полюсы разомкнутой системы. Соответствующая этому изменению функция

(2.9.41)

легко может быть вычислена.

Участок III – это участок движения комплексной переменной вдоль окружности бесконечно малого радиуса с центром в начале координат, где по условию находится 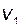полюсов передаточной функции разомкнутой системы. При этом, в соответствии с (2.9.33), функция 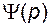будет иметь вид

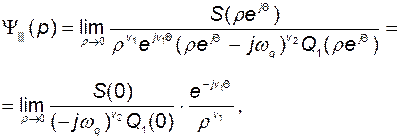(2.9.42)

то есть на плоскости 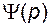будет иметь место перемещение («доворот») по окружности бесконечно большого радиуса. Направление этого перемещения противоположно по знаку направлению перемещения на плоскости , а абсолютная величина приращения угла - в 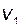раз больше. Таким образом, третьему участку соответствует изменение фазы функции 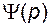на величину

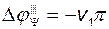. (2.9.43)

Наконец, рассмотрим движение комплексной переменной вдоль окружности бесконечно малого радиуса с центром в точке 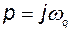, где расположено 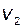полюсов передаточной функции разомкнутой системы. На этом, четвертом участке контура С,

. (2.9.44)

В соответствии с (2.9.33) функция

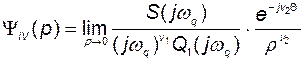(2.9.45)

будет образовывать годограф, перемещающийся на плоскости 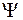по окружности бесконечно большого радиуса, и соответствующее приращение фазы будет равно

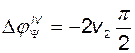. (2.9.46)

Пользуясь тем, что 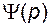является дробно–рациональной функцией от , и

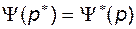, (2.9.47)

можно произвести обход лишь верхней половины контура . Тогда суммарное приращение фазы

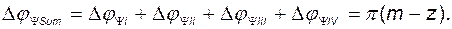(2.9.48)

Удобнее строить не функцию 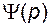, а функцию 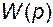. Как видно из равенства (2.9.34), годограф функции 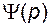поворачивается вокруг начала координат на тот же угол, что и годограф функции 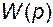поворачивается относительно точки .

Вышеприведенные рассуждения позволяют сформулировать критерий устойчивости замкнутой системы, который называют частотным критерием, или критерием Найквиста.

Дата добавления: 2015-03-31