Модальная (спектральная) интерпретация решения векторно-матричных дифференциальных линейных стационарных уравнений

Рассмотрим сначала движение автономной системы

. (2.5.12)

Пусть все собственные числа матрицы различны. Тогда ее собственные векторы образуют базис в пространстве , то есть являются линейно независимыми. В соответствии с (2.3.5) и (2.4.28) решение уравнения (2.5.12) можно записать в виде

.

Обозначим скаляр

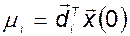, (2.5.13)

тогда

(2.5.14)

Очевидно, что свободное движение вектора состояния объекта является комбинацией движений по собственным векторам матрицы . Такие движения называют модами системы, а матрицу собственных векторов - модальной матрицей. Коэффициент 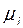соответствует величине возбуждения i - й моды системы, обусловленной начальными условиями. Иначе говоря, каждая мода возбуждается соответствующим выбором начального состояния.

Согласно (2.5.13),

.

Если вектор начальных условий 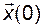совпадает по направлению с i - м собственным вектором, то есть

,

то, учитывая, что согласно (2.4.13) и (2.4.14), при и , получаем

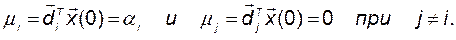
Таким образом, при указанном выборе начальных условий возбуждается только i-я мода, или «частота».

Рассмотрим с этих же позиций движение неавтономного объекта

Изложенный подход можно использовать и в этом случае, если вектор разложить по собственным векторам матрицы :

(2.5.15)

Для того чтобы определить скалярные функции , умножим обе части этого равенства слева на :

откуда, учитывая (2.4.13) и (2.4.14), получаем

(2.5.16)

Таким образом, в соответствии с формулой Коши (2.3.18) и выражением для переходной матрицы (2.4.28) имеем

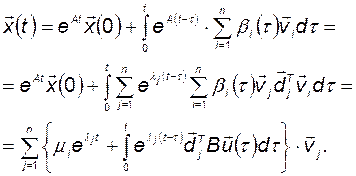(2.5.17)

Если вынуждающая функция выбирается таким образом, чтобы вектор совпадал с направлением одного из собственных векторов матрицы , то она будет возбуждать только одну соответствующую моду - «частоту».

Дата добавления: 2015-03-31