
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однородные дифференциальные уравнения
|
|
|
|
Линейные системы, заданные обыкновенными дифференциальными уравнениями в нормальной форме Коши
Рассмотрим прежде всего решение однородного векторно-матричного дифференциального уравнения
 , (2.3.1)
, (2.3.1)
где каждому начальному условию 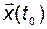 соответствует одно и только одно решение дифференциального уравнения. Будем полагать, что матрица
соответствует одно и только одно решение дифференциального уравнения. Будем полагать, что матрица  непрерывна на промежутке
непрерывна на промежутке 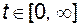 . Множество всех решений образует n-мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых.
. Множество всех решений образует n-мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых.
Это может быть сделано следующим образом. Зададим начальные условия 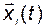 , где
, где  , совпадающие с базисными векторами
, совпадающие с базисными векторами  пространства
пространства  , то есть
, то есть  . Из свойства единственности решений дифференциальных уравнений (через любую точку пространства состояний проходит одна и только одна траектория) следует линейная независимость решений с указанными начальными условиями. Матрица
. Из свойства единственности решений дифференциальных уравнений (через любую точку пространства состояний проходит одна и только одна траектория) следует линейная независимость решений с указанными начальными условиями. Матрица 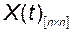 , столбцами которой являются
, столбцами которой являются 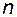 линейно независимых решений системы (2.3.1), называется фундаментальной матрицей этой системы дифференциальных уравнений.
линейно независимых решений системы (2.3.1), называется фундаментальной матрицей этой системы дифференциальных уравнений.
Поскольку каждый столбец фундаментальной матрицы является решением системы (2.3.1), то фундаментальная матрица удовлетворяет уравнению
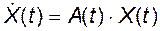 , при начальных условиях
, при начальных условиях 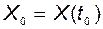 . (2.3.2)
. (2.3.2)
По определению в любой момент времени столбцы этой матрицы линейно независимы, значит, ее определитель (определитель Вронского) не равен нулю на промежутке 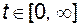 . Так как определитель матрицы
. Так как определитель матрицы  не равен нулю, то существует обратная матрица
не равен нулю, то существует обратная матрица  . Матрица
. Матрица
 (2.3.3)
(2.3.3)
называется переходной матрицей уравнения (2.3.1) или переходной матрицей, соответствующей матрице  . Переходная матрица является определяющей при анализе и решении дифференциальных уравнений и собственно в теории управления. Поэтому ниже приводятся основные её свойства, в основном непосредственно вытекающие из определения этой матрицы.
. Переходная матрица является определяющей при анализе и решении дифференциальных уравнений и собственно в теории управления. Поэтому ниже приводятся основные её свойства, в основном непосредственно вытекающие из определения этой матрицы.
1). Переходная матрица при совпадающих значениях первого и второго аргумента становится единичной матрицей:
 .
.
2). При любых значениях аргументов 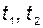 переходная матрица
переходная матрица 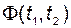 не вырождена и её определитель не равен нулю:
не вырождена и её определитель не равен нулю:
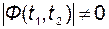 .
.
3). Обращение матрицы  эквивалентно изменению порядка аргументов исходной матрицы:
эквивалентно изменению порядка аргументов исходной матрицы:
 .
.
4). Если в качестве фундаментальной матрицы начальных условий принять единичную матрицу,  , то при всех прочих t переходная матрица будет совпадать с фундаментальной матрицей.
, то при всех прочих t переходная матрица будет совпадать с фундаментальной матрицей.
 . Но
. Но 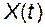 – это решение матричного дифференциального уравнения (2.3.2). Поэтому переходная матрица может быть определена как решение матричного дифференциального уравнения:
– это решение матричного дифференциального уравнения (2.3.2). Поэтому переходная матрица может быть определена как решение матричного дифференциального уравнения:

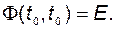 (2.3.4)
(2.3.4)
5). Переходная матрица определяет решение однородного векторно-матричного дифференциального уравнения (2.3.1), удовлетворяющее начальному условию  :
:
 . (2.3.5)
. (2.3.5)
Это действительно так, ибо, во-первых, при 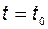
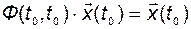 ,
,
во-вторых, с учетом свойства (4):
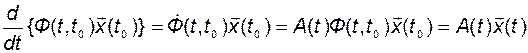 .
.
6). Из предыдущего свойства следует один из способов определения переходной матрицы. Обозначим через  элемент i-й строки и j-го столбца переходной матрицы и запишем равенство (2.3.5) в развернутом виде:
элемент i-й строки и j-го столбца переходной матрицы и запишем равенство (2.3.5) в развернутом виде:
 ,
,
откуда следует выражение для i-й координаты вектора состояния:
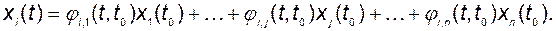
Если положить начальные условия по всем координатам вектора состояния, кроме j-й, нулевыми, а по j-й - единичными, то есть
 при
при 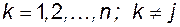 и
и  , (2.3.6)
, (2.3.6)
то элемент i-й строки и j-го столбца матрицы  можно определить как процесс по i-й координате вектора состояния:
можно определить как процесс по i-й координате вектора состояния:
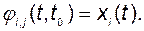 (2.3.7)
(2.3.7)
7). К переходной функции применимо правило композиции:
 (2.3.8)
(2.3.8)
Действительно, решение уравнения (2.3.1) в момент t1 при начальных условиях 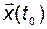 имеет вид
имеет вид

Если теперь этот результат принять за новые начальные условия, то к моменту времени  будем иметь:
будем иметь:

8). Переходная матрица может быть вычислена с помощью ряда Пеано, или матрицианта матрицы  :
:
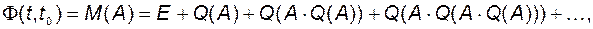
где
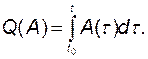
Для того чтобы получить этот результат, проинтегрируем дифференциальное уравнение (2.3.1):
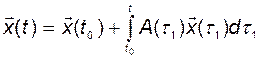 .
.
Теперь повторим эту процедуру многократно, учитывая, что

Тогда получим
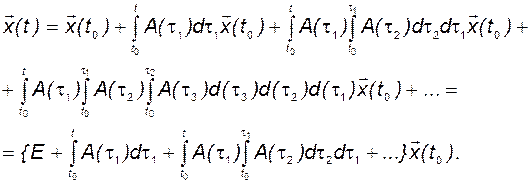
Если объект – стационарный и матрица А состоит из постоянных и не зависящих от времени элементов, то матрициант матрицы А (или ряд Пеано) превращается в выражение для матричной экспоненты:
 (2.3.9)
(2.3.9)
Очевидно, что в стационарном случае переходная матрица является уже функцией только одного аргумента, равного разности начального и текущего (конечного) времени:
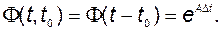 (2.3.10)
(2.3.10)
Переходная матрица для стационарного объекта обладает рядом дополнительных замечательных свойств, трансформирующихся из соответствующих свойств переходной матрицы для нестационарного объекта:
из 1) -  ; (2.3.11)
; (2.3.11)
из 3) -  ; (2.3.12)
; (2.3.12)
из 4) - 
 ; (2.3.13)
; (2.3.13)
из 5) - решение однородного дифференциального уравнения имеет вид
 ; (2.3.14)
; (2.3.14)
из 7) -  . (2.3.15)
. (2.3.15)
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 508; Нарушение авторских прав?; Мы поможем в написании вашей работы!