Линеаризация исходных уравнений

Почти все реальные объекты и системы автоматического управления являются нелинейными. Однако среди нелинейных функци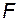й и 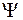часто встречаются такие, которые при определённых допущениях в рабочей области функционирования системы могут быть заменены линейными. В качестве примера такого случая представлена элементарная функция на рис.2.2. В данном случае возможна линеаризация, так как если точка перемещается на небольшие расстояния по кривой 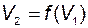, то этот участок кривой можно заменить отрезком прямой. В то же время нелинейная функция на рис.2.3 не допускает подобную замену, если в процессе работы системы происходит изменение уровня выходного сигнала . Системы с такого типа функциями называют существенно нелинейными. Их исследованию будет посвящен специальный раздел пособия. Ниже будет рассмотрен класс систем, допускающих линеаризацию.

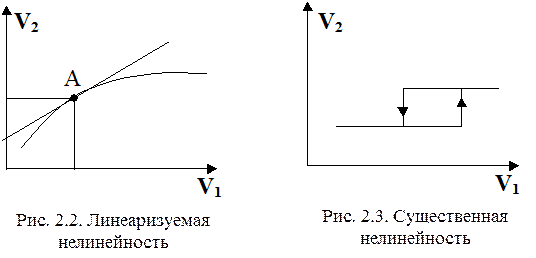
Пусть режим функционирования объекта определяется некоторой траекторией по вектору управления , а действительная реализация 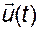близка к ней:

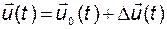. (2.2.1)

При этом решение уравнения (2.1.3) можно записать в виде

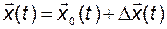, (2.2.2)

где 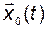– решение уравнения (2.1.3) при .

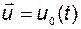Назовём функционирование объекта (системы) при 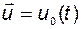базовым режимом. Переменные 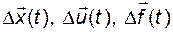– это отклонения от соответствующих переменных в базовом режиме.

Подставим теперь выражения для 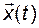и 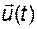в исходное дифференциальное уравнение состояний

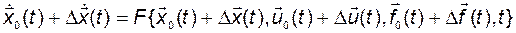
и разложим функцию 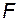в ряд Тейлора:

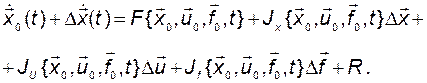(2.2.3)

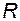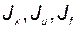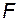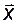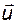Здесь – остаточный член, содержащий высшие степени приращений, и им можно пренебречь; – матрицы Якоби функции для , и .

Элемент матрицы Якоби определяется как со­от­вет­ствующая частная производная 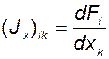. Например, для системы второго порядка соответствующее слагаемое в правой части (2.2.3) имеет вид

.

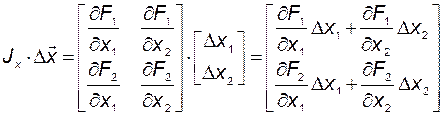Пренебрегая в (2.2.3) остаточным членом 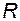и учитывая уравнение для базового режима, получим

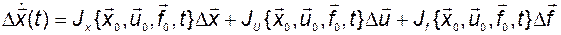. (2.2.4)

Введем обозначения:

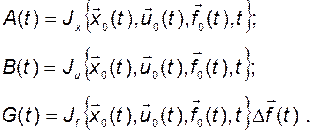
В результате получим:

линейное дифференциальное векторно-матричное уравнение с переменными параметрами (коэффициентами)

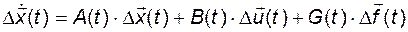. (2.2.5)

Аналогичным образом проведем линеаризацию уравнения вы­хо­да:

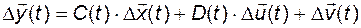. (2.2.6)

Впредь, рассматривая линейные модели системы, будем опускать сим­вол D при записи приращений соответствующих векторов. Таким образом, линеаризованные уравнения объекта (системы) примут вид

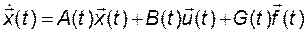; (2.2.7)

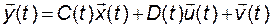. (2.2.8)

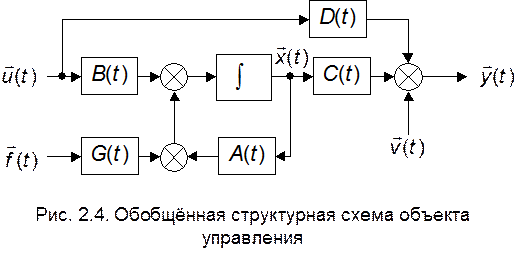
Ha рис. 2.4 приведена структурная схема, являющаяся графичес­ким изображением уравнений (2.2.7) и (2.2.8).

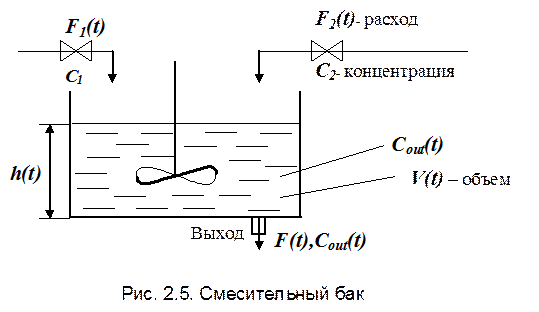
В качестве примера рассмотрим смесительный бак, который напол­няется с помощью двух потоков, имеющих переменные мгновенные расходы 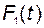и 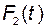(рис. 2.5). Оба входных потока содержат раство­римое вещество с неизменными концентрациям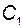и и 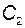. Выходной поток имеет массовую скорость истечения (мгновенный расход) 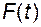. Пред­полагается, что содержимое бака перемешивается так, что концентра­ция выходного потока равна концентрации 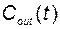в баке.

Запишем уравнения баланса масс в баке.

Для полной массы:

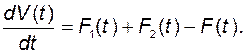(2.2.9)

Для массы растворённого вещества:

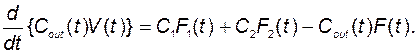(2.2.10)

Мгновенный расход выходного потока при естественном истечении зависит от уровня жидкости в баке 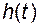следующим образом:

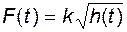, (2.2.11)

где - некоторая константа. Это следует из уравнения Бернулли, которое описывает энергетический баланс жидкости перед сливным отверстием и после него. Потенциальная энергия жидкости перед сливным отверстием пропорциональна 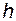. При истечении из бака энергия жидкости превращается в кинетическую энергию потока, пропорциональную квадрату скорости 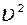. Приравнивая эти энергии, получаем 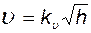. Расход 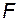пропорционален произведению скорости истечения на площадь сливного отверстия, откуда и следует (2.2.11).

Если бак имеет постоянную по высоте площадь поперечного сечения , то

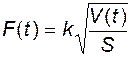. (2.2.12)

Тогда из (2.2.9) и (2.2.10) получаем

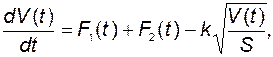
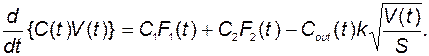
Выберем в качестве базового режима установившееся состояние (статику), когда все величины являются постоянными - 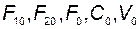. При этом из предыдущих уравнений получаем

,

.

.

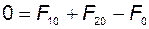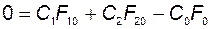При известных 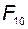и 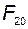эти уравнения могут быть разрешены относи­тельно 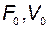и :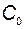

.

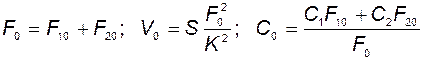Предположим теперь, что возникли отклонения от установившегося состояния:

,

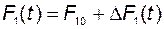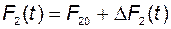
и, как следствие,

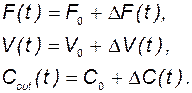
Если эти отклонения невелики, то можно провести линеаризацию нелинейных дифференциальных уравнений объекта.

Снача­ла линеаризуем уравнение для полной массы

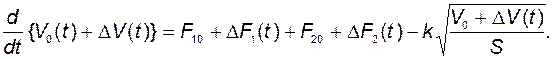
Используем разложение нелинейной функции в ряд Тейлора и учтём, что

.

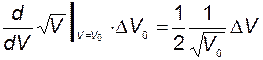Тогда

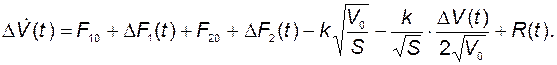
Учитывая уравнение статики и пренебрегая остаточным членом, получим

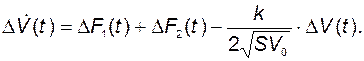(2.2.13)

Введём параметр 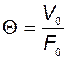, называемый временем заполнения бака. Тогда, учитывая (2.2.12), получим

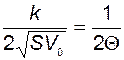. (2.2.14)

Кроме того, отметим, что

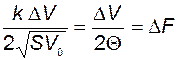. (2.2.15)

Таким образом, вместо (2.2.13) запишем

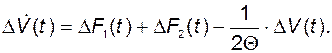(2.2.16)

Проведем аналогичные действия для уравнения баланса масс раст­во­рён­ного вещества.

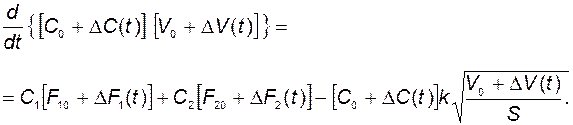
После разложения в ряд Тейлора получим

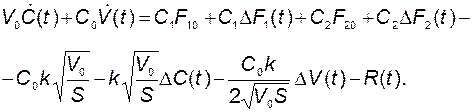
Учтём уравнения статики и отбросим остаточный член:

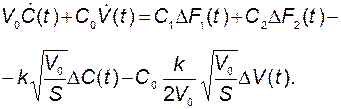
Подставим в это уравнение 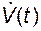из (2.2.16). Получим

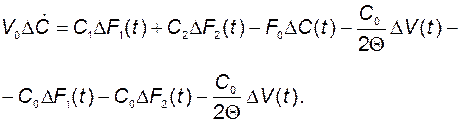
Таким образом, в результате линеаризации мы получили систему следующих дифференциальных уравнений, которые описывают процессы в смесительном баке:

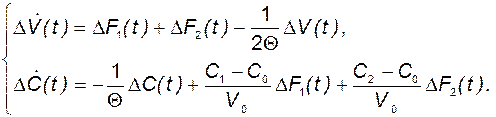(2.2.17)

На этом завершён для данного примера первый этап разработки - составлено математическое описание объекта и в результате линеаризации получена его линейная модель. Далее это описание нужно представить в удобной форме - в виде векторно-матричных дифференциальных уравнений и в виде структурной схемы.

Представим математическое описание объекта в виде векторно-матричных дифференциальных уравнений. Введем обозначения:

.

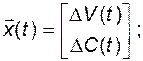
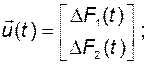
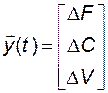Теперь систему уравнений (2.2.17) можно записать в векторно-матричном виде:

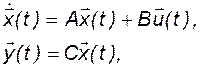
где

; ; .

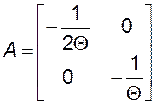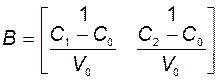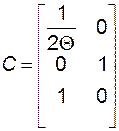Структурная схема объекта представлена на рис.2.6.

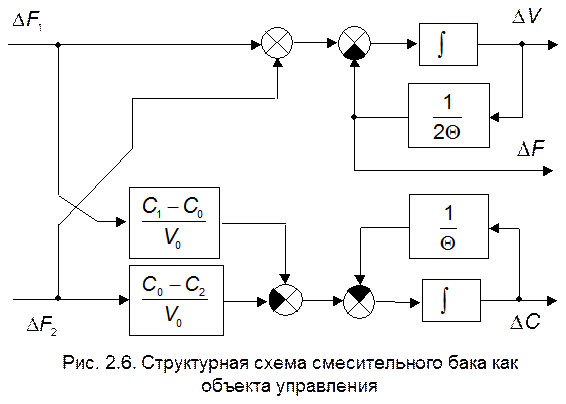
На основании полученных дифференциальных уравнений и структурной схемы можно провести предварительный анализ свойств объекта и сделать следующие выводы.

1. Изменение любой из входных переменных 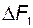и 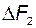приводит к одновременному изменению всех выходных переменных 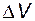, 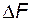и 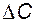. Это особенно наглядно следует из наличия перекрёстных связей на структурной схеме объекта.

2. При ступенчатом изменении любой из входных переменных каждая из выходных переменных изменяется по экспоненциальному закону, причём темп изменения концентрации 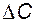вдвое медленнее темпа изменения объёма .

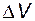Предметом отдельного рассмотрения при проектировании системы управления (СУ) должен стать анализ диапазонов изменения переменных объекта, в которых сохраняется адекватность линейной модели.

Прежде, чем закончить рассмотрение данного примера, имеет смысл продемонстрировать некоторые последующие действия разработчика в части синтеза алгоритмов управления. Перед разработчиком среди прочих встанут следующие две задачи. Одна из них - обеспечение заданных требований по длительности и качеству процессов в системе, то есть её динамических свойств. Рассмотрению соответствующих вопросов посвящён третий раздел настоящего пособия.

Вторая задача - обеспечение возможности независимого управления объёмом и концентрацией. Введём понятие командных сигналов по требуемым концентрации - 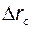и объёму - 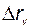. В статике производные всех переменных должны быть равны нулю и, как следует из структурной схемы и дифференциальных уравнений объекта, должны выполняться равенства

;

.

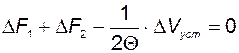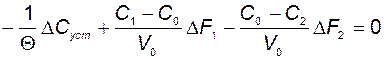Отсюда, с учётом равенства 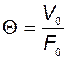, получаем

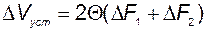; (2.2.18)

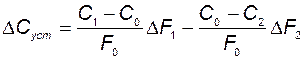. (2.2.19)

Для компенсации перекрёстных связей в объекте введём перекрёстные связи в регуляторе:

;

.

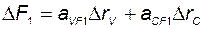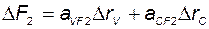Подставим эти выражения в (2.2.18) и (2.2.19):

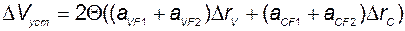; (2.2.20)

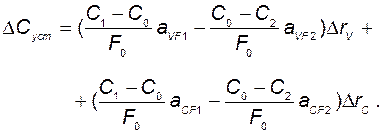(2.2.21)

Для того чтобы установившееся значение объёма жидкости в баке 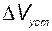определялось только командным сигналом 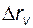и не зависело от 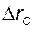, а выходная концентрация 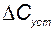определялась только командным сигналом 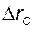и не зависела от 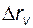, в равенстве (2.2.20) приравняем к нулю коэффициент при 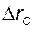, а коэффициент при 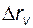приравняем к единице. В равенстве (2.2.21) приравняем к нулю коэффициент при 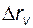, а коэффициент при 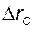приравняем к единице. В результате решения получившейся системы уравнений получим

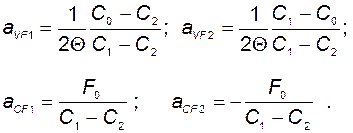(2.2.22)

В итоге получаем представленную на рис.2.7 структурную схему системы управления смесительным баком, в которой обеспечена развязка каналов. Последнее означает, что командный сигнал 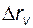влияет только на изменение объёма жидкости в баке, а командный сигнал 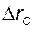- только на изменение концентрации. Объём жидкости в баке связан с расходом выходного потока 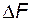коэффициентом пропорциональности 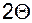, поэтому регулирование первого можно рассматривать как регулирование второго.

Дата добавления: 2015-03-31