Понятие пространства состояний

Методы анализа непрерывных систем

С точки зрения анализа и синтеза систем все переменные, характеризующие объект управления (рис.2.1) или имеющие к нему отношение, делятся на три группы.

1.Входные воздействия, представляющие сигналы, генерируемые сис­темами, внешними по отношению к исследуемому объекту, и влияющие на его поведение. Внешние сигналы разделяют на сигналы управляющие - и возмущающие - .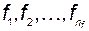

2.Выходные переменные, или переменные, позволяющие описать не­которые аспекты поведения объекта, представляющие интерес для иссле­дователя или потребителя результатов функционирования объекта - .

3.Переменные состояния, или промежуточные переменные 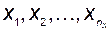, характеризующие динамическое поведение исследуемого объек­та или системы.

Для удобства оперирования с многомерными величинами совокупность управляющих переменных представляют в виде вектора управления 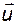. Аналогичным образом вводятся понятия вектора возмущения , вектора выхода и вектора состояния :

, , , .

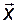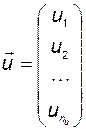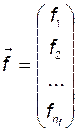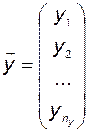Множество всех значений, которые может принять вектор 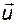в момент времени , образует пространство управления. Аналогично вводятся понятия пространства возмущений, пространства выходов и пространства состояний.

В любой момент времени состояние системы является функцией начального состояния 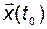и векторов 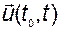и . Если известно, как изменялись эти векторы на интервале 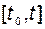, то однозначно может быть определено состояние системы :

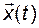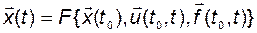. (2.1.1)

Вектор выхода в момент времени является функцией тех же переменных:

. (2.1.2)

Состояние системы отделяет будущее от прошлого, так что состо­яние содержит всю информацию, необходимую для определения реакции объекта на произвольный входной сигнал. Понятие состояния является основным исходным понятием и, следовательно, не может быть определено более полно, чем, например, слово "множество" в математике. Наибольшее, что можно сделать, это сформулировать свойства, какими должна обладать система, поведение которой отвечает понятию состо­яния.

Основным свойством состояния является то, что будущие значения его не зависят от характера достижения системой её текущего состо­яния. Состояние системы в данный момент времени, а также текущее и будущие значения её входов единственным образом определяют настоя­щее и будущие значения её состояния и выходов.

Уравнение (2.1.1) называют уравнением состояния системы, а уравне­ние (2.1.2) - уравнением выхода. Если объект описывается дифференциаль­ным уравнением, то уравнения (2.1.1) и (2.1.2) превращаются в

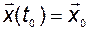, ; (2.1.3)

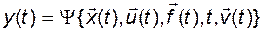, (2.1.4)

где дополнительно введён вектор ошибок измерений .

Как правило, выбор состояния естественным образом следует из физического устройства системы, а уравнение (2.1.3), называемое диффе­ренциальным уравнением состояния, обычно следует из элементарных физических законов, которыми определяется её поведение.

Дата добавления: 2015-03-31