Матричная весовая и переходная функции

Свойства движений линейных систем

Пусть заданы уравнения некоторого динамического объекта

; (2.5.1)

. (2.5.2)

В соответствии с формулой Коши выражение для вектора выхода

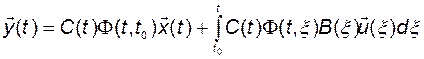. (2.5.3)

Анализируя качество работы объекта, удобно рассматривать движение как сумму свободной составляющей, обусловленной в основном свойствами самого объекта, и вынужденной составляющей, несущей отпечаток входного сигнала - вектора управления. Строго говоря, это разделение условно, но очевидно, что свободную составляющую целесообразно отождествить с первым слагаемым правой части равенства (2.5.3). Отсюда следует вывод, что основные свойства объекта определяются его переходной матрицей 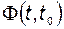, в то время как степень их проявления зависит от вектора начальных условий.

Отметим, однако, что первопричиной всякого движения объекта является вектор управления. Это означает, что даже при анализе собственных движений объекта следует учитывать и матрицу управления .

Обозначим

. (2.5.4)

Очевидно, что для 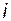-й координаты вектора выхода при нулевых начальных условиях справедливо выражение

.

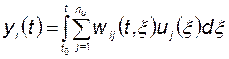Если положить

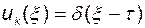
и при , то в соответствии со свойствами -функции получим

.

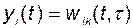Таким образом, элемент, стоящий в 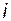-й строке и в -м столбце матрицы , можно интерпретировать как реакцию 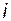-й координаты вектора 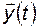на дельта-функцию в -й координате вектора управления .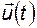

Матрица называется матричной весовой или матричной импульсной переходной функцией объекта по вектору выхода. Аналогич­ным образом определяется матричная весовая функция объекта по вектору состояния

. (2.5.5)

Интеграл от матричной весовой функции

(2.5.6)

называют матричной переходной функцией объекта. Элементы этой матрицы могут рассматриваться как реакции координат вектора выхода (вектора состояния) на единичные функции по соответствующим координатам вектора управления. Если на вход объекта поступает постоянный во времени вектор управления 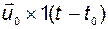, то при нулевых начальных условиях

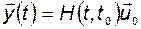. (2.5.7)

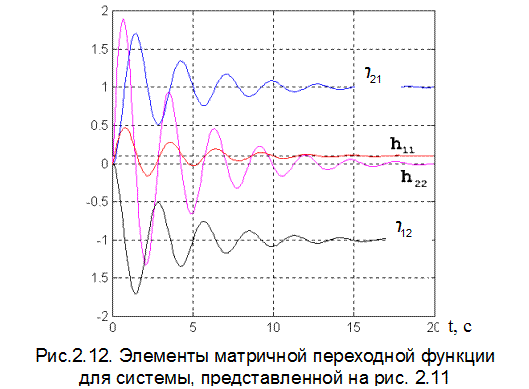
В качестве примера на рис. 2.12 изображены элементы матричной переходной функции по вектору состояния для системы, представленной на рис. 2.11.

В стационарном случае рассмотренные матрицы являются функцией одного аргумента:

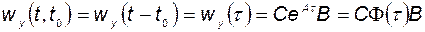(2.5.8)

и

. (2.5.9)

Это выражение для переходной функции можно упростить. Производя замену аргумента

,

получим

и окончательно

. (2.5.10)

Используя представление переходной матрицы через матричную экспоненту, можно получить

. (2.5.11)

Один из наиболее употребимых способов вычисления 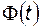и 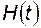состоит в определении (расчете) соответствующих окаймленных матричных рядов.

ПРИМЕР 2.5.1. Объект управления соответствует схемой в переменных состояния, приведенной на рис. 2.13.

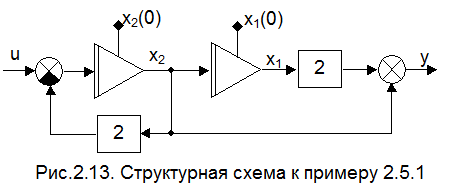
Этой схеме соответствуют уравнения

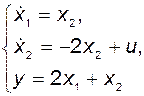
Требуется найти переходную матрицу, матричные весовую и переходную функции, реакцию объекта на постоянный входной сигнал.

Прежде всего, найдем переходную матрицу. Элемент первой строки и первого столбца этой матрицы можно определить как реакцию координаты 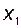на начальные условия при 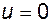. Решение первого дифференциального уравнения дает

Аналогично

при .

Решая при этих условиях второе дифференциальное уравнение, получим

.

Очевидно, 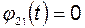, так как координата 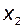не зависит от 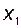. Для того чтобы определить 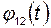, следует взять интеграл

.

Таким образом,

.

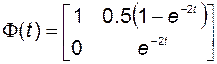В соответствии с уравнениями объекта

,

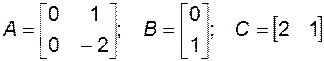поэтому

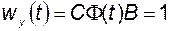
и

.

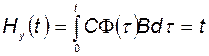При нулевых начальных условиях и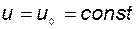

.

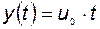Если начальные условия ненулевые, то

.

При этом

Видно, что в выходной координате участвуют не все составляющие движения, присутствующие в векторе состояния. Еще более характерная ситуация возникнет, если изменить исходные данные. Если положить

то поведение выходной координаты принципиально не изменится:

,

но процесс по координатам состояния будет неограниченно расти:

.

Такие случаи, когда вектор выхода не отражает характерные свойства объекта, могущие привести к катастрофическим результатам, будут подробно обсуждаться в последующих разделах.

Дата добавления: 2015-03-31