Собственные значения и собственные векторы транспонированной матрицы

Собственные значения транспонированной матрицы - это такие 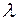, для которых система уравнений

(2.4.7)

имеет нетривиальные решения, т.е. когда

. (2.4.8)

Решение этого алгебраического уравнения дает значений собственных чисел 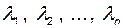. Так как определители квадратной матрицы и её транспонированной матрицы равны, то собственные числа матриц 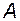и 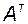также равны.

Таким образом, собственному числу соответствует собственный вектор матрицы 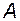и собственный вектор матрицы .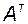

Если транспонировать обе части уравнения (2.4.7), то получим

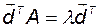. (2.4.9)

В связи с этим вектор называют левым собственным вектором матрицы 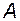, в отличие от 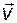, который, в таком случае, называют правым собственным вектором. Для 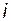-го собственного числа и 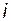-го левого собственного вектора соответственно

.

Умножим обе части этого равенства справа на вектор :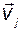

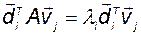. (2.4.10)

Учитывая свойства собственных векторов, в результате получаем уравнение

,

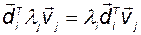которое преобразуется к виду

. (2.4.11)

Полагаем, что все собственные числа матрицы 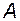различны. Тогда для имеем и из равенства (2.4.11) следует, что векторы и взаимно ортогональны:

. (2.4.12)

Это означает то, что 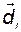ортогонален - мерной гиперплоскости с базисом, образованным векторами для всех .

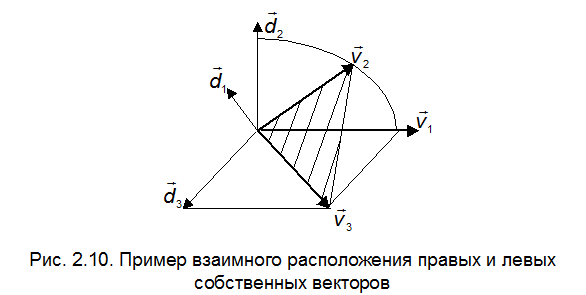
В качестве примера на рис. 2.10показан один из вариантов взаимного расположения правых и левых собственных векторов некоторой матрицы 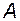для случая . Здесь хорошо видно, что каждый из векторов ортогонален всем векторам при .

Теперь рассмотрим случай, когда 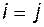. При этом скалярные произведения векторов и 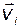не должны быть равны нулю. Если предположить, что 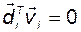, то придется утверждать, что вектор ортогонален всему n – мерному пространству с базисом 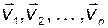. Но этого не может быть, так как вектор сам принадлежит этому пространству. Таким образом,

для . (2.4.13)

В связи с тем, что собственные векторы можно выбирать с точностью до постоянного (в том числе комплексного) сомножителя, то наборы, иначе говоря, базисы 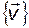и 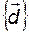формируют так, чтобы для 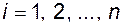выполнялось условие

. (2.4.14)

Отметим ещё одно важное свойство собственных векторов:

Если матрица 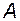не имеет кратных собственных чисел, то все её собственные векторы линейно независимы, то есть образуют базис в пространстве .

Это нетрудно доказать. Действительно, предположим сначала, что среди собственных векторов матрицы 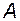первые два являются линейно зависимыми, то есть

, (2.4.15)

где ни один из коэффициентов 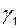и 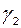не равен нулю. Умножив это уравнение слева на 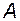, получим

. (2.4.16)

Теперь умножим (2.4.15) на :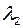

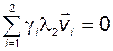. (2.4.17)

Вычтем (2.4.17) из (2.4.16) и в результате получим

.

Из того, что 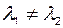и , следует , чего не может быть, следовательно, первые два собственных вектора не могут быть линейно зависимыми.

Теперь предположим, что число линейно зависимых векторов равно , то есть

.

Умножив это уравнение слева на 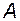, получим

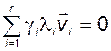. (2.4.18)

Умножим (2.4.18) на :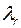

. (2.4.19)

Вычтем (2.4.19) из (2.4.18) и в результате будем иметь

.

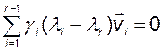Получается, что число линейно зависимых векторов . Если согласиться с этим, то дойдём до , и круг замкнулся.

Таким образом, действительно, все собственные векторы матрицы 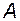являются линейно независимыми, поэтому матрица 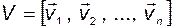, построенная из векторов базиса 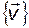, т.е. из правых собственных векторов матрицы 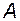, является невырожденной. Эта матрица называется модальной матрицей. Из перечисленных выше свойств для правых и левых собственных векторов следует равенство

, или , (2.4.20)

где 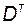- матрица, строки которой являются транспонированными векторами двойственного базиса 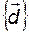, т.е. левыми собственными векторами матрицы :

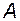. (2.4.21)

2.4.3.Определение функции от матрицы через её левые и правые собственные векторы

Все n систем уравнений

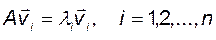
могут быть записаны с использованием блочных матриц:

.

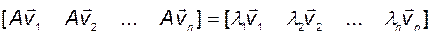Учтем, что

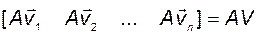
и

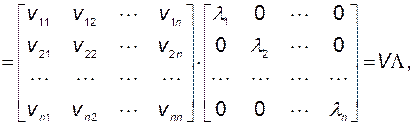
где - диагональная матрица собственных чисел.

Таким образом, получено равенство

,

или

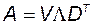. (2.4.22)

Преобразовани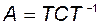е , где - произвольная невырожденная матрица, называется преобразованием подобия. Одно из основных свойств этого преобразования заключается в том, что собственные числа подобных матриц (здесь - 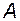и ) совпадают. Действительно,

.

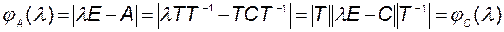Говорят, что матрица 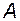приводится к диагональному виду преобразованием

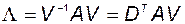. (2.4.23)

Более высокие степени 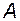приводятся к диагональному виду таким же способом:

.....................................................

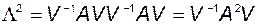
или .

Таким образом, если рассмотреть матричный многочлен

то

или

. (2.4.24)

Если применить этот результат к характеристическому полиному, то получим

(2.4.25)

то есть каждая квадратная матрица удовлетворяет своему харак­те­ри­сти­ческому полиному. Это утверждение известно в теории матриц как теорема Кэли-Гамильтона.

Для любой функции от матрицы , которую можно представить в виде конечного или бесконечного степенного полинома, справедливо аналогичное выражение

(2.4.26)

или эквивалентное ему

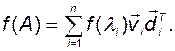(2.4.27)

Отсюда вытекает, например, один из способов определения матричной экспоненты или соответствующей переходной матрицы:

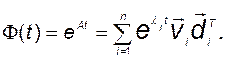(2.4.28)

ПРИМЕР 2.4.2. Для объекта, представленного на рис.2.8 в примере 2.4.1, найдём левые собственные векторы. Если обозначить присоединённую матрицу к матрице 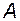как 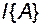, то очевидно равенство

.

Поэтому

.

Учитывая, что

,

имеем

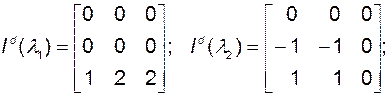
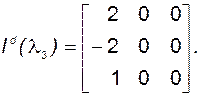
Рассчитаем левые собственные векторы. Учтем при этом (2.4.14). Таким образом, для первого собственного вектора должны выполняться условия

,

откуда

и .

Аналогично получим

.

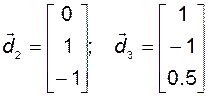Теперь можно записать выражение для переходной матрицы. Из (2.4.28) имеем

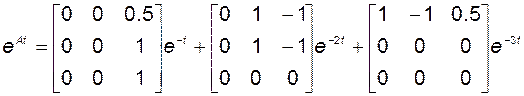
и окончательно

.

Рассмотрим ещё несколько примеров.

Для

имеем

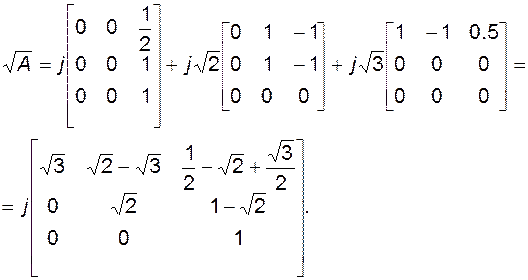
Проведём проверку:

Для той же матрицы найдём :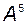

и

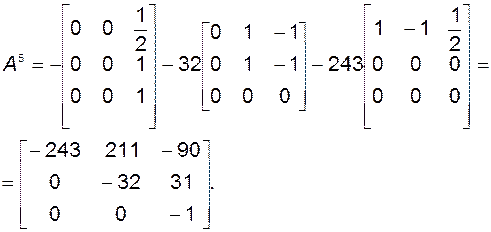
Дата добавления: 2015-03-31