Теорема доказана

В многоугольник можно вписать окружность, если найдется точка, равноудаленная от всех его сторон. Эта точка лежит на биссектрисе каждого угла многоугольника. Следовательно, в многоугольник можно вписать окружность тогда и только тогда, когда биссектрисы всех его углов имеют общую точку. Эта точка и будет центром вписанной окружности.

Около многоугольника можно описать окружность, если найдется точка, равноудаленная от всех его вершин. Эта точка лежит на серединном перпендикуляре каждой стороны многоугольника. Следовательно, около многоугольника можно описать окружность тогда и только тогда, когда серединные перпендикуляры всех его сторон имеют общую точку. Эта точка и будет центром описанной окружности.

Отсюда

За длину окружности принимается тот предел, к которому стремится (приближается) переменный периметр правильного многоугольника, вписанного в эту окружность, когда число его сторон неограниченно удваивается.

Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности. Из определения окружности следует, что все радиусы имеют равную длину. Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Из чертежа очевидно, что площадь сектора зависит от градусной меры центрального угла, образованного радиусами, ограничивающими данный сектор. Она может быть определена как соответствующая часть площади руга.

1.

Словарный состав языка.

Аналитические способы выражения грамматического значения.

Аналитические способы выражения грамм. значений:

1) Супплетивизм – соединение в одну грамматическую пару разнокорневых слов, когда, несмотря на различие корней, лексическое знач-ие не меняется, а разнокорневые слова служат для различения грамм. значений. Для рус.яз. этот способ не продуктивен: множественное число сущ-ых,глаг-ах, метоим-ях (напр., идти/шёл, есть/был/буду, я/меня)

2) Синтаксическая связь применяется для выражения грамм. знач-ий тех слов, у которых нет формы изменения, когда применяются другие слова, с которыми данное слово сочетается в предложении (напр., в зоопарке новый шимпанзе/в зоопарке много шимпанзе.

3) Порядок слов в предложении. Линейность речи позволяет рассматривать её, как некую последовательность действий во времени (если речь идёт о письме, то ещё и в пространстве). Порядок расположения последовательности может иметь огромное значение. Для разны языков различно: есть языки, в которых порядок слов в предложении строго закреплён.

4) Интонация.

Все слова, существующие в языке, образуют его словарный состав. Наиболее часто активно употребляемые слова составляют его основной словарный фонд.

Словарный состав языка дифференцируется по разным признакам.

Основной словарный фонд состоит из активного словаря (все слова, которые мы понимаем и активно употребляем) и пассивного словаря (он более широкий, включает в себя слова, которые мы понимаем, но не используем).

Лексика представляет собой систему:

1. Неологизмы – слова, возникшие на памяти применяющего их поколения:

а) лексические (просто новые появившиеся),

б) семантические (к существующему в языке слову добавляется новое значение, напр., спутник – космич./приятель)

2. Заимствования:

а) калькирование (телевидение),

б) интернационализмы (гео, гидра и т.д.). Полезны или вредны? Считают, что заимствоваться должны лишь те слова, аналогов которых нет в данном языке, а те, которые уже есть, заимствовать и использовать не надо.

3. Архаизмы – устаревшие слова (уходят из языка, т.к. уходят из обращения (употребления) слова, которые они обозначают, на смену приходят другие слова).

4. Историзмы – слова, которые обозначали различные исторические предметы/явления (барин, штабс-капитан)

5. Эвфемизмы – слова, которые используются вместо неких табуированных (запрещённых) слов.

а) Не будет, потому что пепсин не действует на указанные аминокислоты.

б) Смотри стрелки под формулой пептида наверху.

в)

г) Азотистый баланс понизится, так как будет угнетён энергетический обмен и произойдёт катаболизм белков.

2. а) Гистидин, Аргинин

б) в)

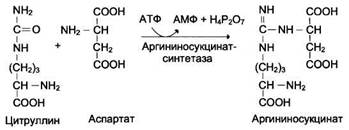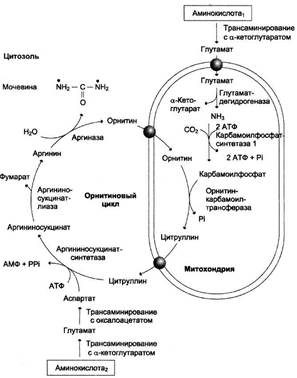
г) Продукт – мочевина.

Значение – выведение аммиака, накопление которого приводит к токсическому эффекту.

3. а) В крови – аммиак, глутамин, ион аммония NH4+, а также метаболиты орнитинового цикла: цитрулит, аргининосукцинат. Наибольшей токсичностью обладают: аммиак, глутамин, ион аммония.

б) Высокие концентрации аммиака стимули­руют синтез глутамина из глутамата в нервной ткани (при участии глутаминсинтетазы): Глутамат + NH₃ + АТФ → Глутамин + АДФ + Н₃РО₄.

Накопление глутамина в клетках нейроглии приводит к повышению осмотического дав­ления в них, набуханию астроцитов и в боль­ших концентрациях может вызвать отёк мозга. Снижение концентрации глутамата нарушает обмен аминокислот и нейромедиаторов, в частности синтез γ-аминомасляной кислоты (ГАМК), основного тормозного медиатора. При недостатке ГАМК и других медиаторов нарушается проведение нервно­го импульса, возникают судороги.

Ион NH₄⁺ практически не проникает через цитоплазматические и митохондриальные мембраны. Избыток иона аммония в крови способен нарушать трансмембранный пере­нос одновалентных катионов Na⁺ и К⁺, кон­курируя с ними за ионные каналы, что также влияет на проведение нервных импульсов.

в) Избегать белковой пищи, введение кетоаналогов аминокислот, стимулирование выведения аммиака в обход нарушенных реакций путём связывания и выведения NH₃ в со­ставе фенилацетилглутамина и гиппуровой кислоты; а также повышением концентрации промежуточных метаболитов цикла (аргинина, цитруллина, глутамата), образующихся вне блокируемых реакций.

4. а) б)

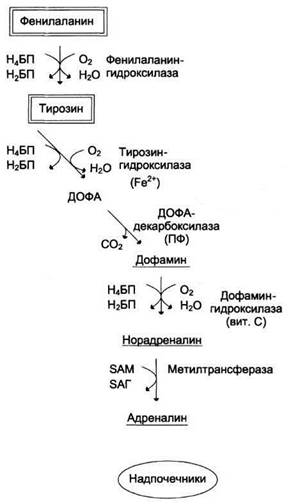
в) Гормон физической работы, который синтезируется при стрессе и регулирует основной обмен, а так же условные сокращения сердечной мышцы.

Место синтеза – мозговое вещество надпочечников.

5. а) Дофамин

б) в)

Кофермент - ФАД

Фермент – ДОФА-декарбоксилаза

Площадь сектора с центральным углом в 1° составляет часть площади круга, а площадь сектора с центральным углом в a° составляет часть площади круга и определяется по формуле: Преобразуем полученную формулу: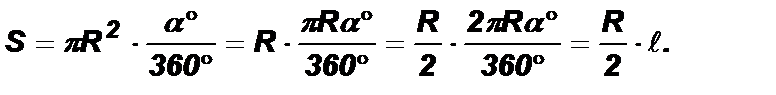

S₁

S₂

S₃

Следует заметить, что площадь вектора однозначно определяется величиной центрального угла. Чем больше центральный угол сектора, тем больше длина дуги и, соответственно, площадь сектора.

С

В

А

B

A

S₁

S₂

O

O

D

Определение 3. Сегментом называется часть круга, ограниченная дугой и хордой, соединяющими концы этой дуги.

Вывод формулы площади сегмента.

Из чертежа очевидно, что площадь сегмента может быть определена:

а) как разность площадей сектора 1 и треугольника AOB, если ÐАОВ < 180°;

б) как сумма площадей сектора 2 и треугольника AOB, если ÐАОВ > 180°.

Если градусная мера дуги АВ (соответствующего ей центрального угла) невелика, то площадь сегмента может быть определена по приближенной формуле: где b – есть основание сегмента или длина хорды АВ, а h – высота сегмента (стрелка сегмента). Стрелкой сегмента называется часть диаметра круга, перпендикулярного его хорде, лежащая в сегменте. h = CD. Если градусная мера дуги не превышает 50°, то погрешность в вычислении площади не превышает 1 %.

22. Доказать формулы длины окружности, длины дуги окружности.

Определение 1. Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.

С₃

С₂

С₁

Теорема 1 (о длине окружности). Длина С окружности радиусом R выражается формулой С = 2pR.

Пусть С и С’ – длины окружностей радиусов R и R’. Впишем в каждую из этих окружностей правильный n-угольник. Тогда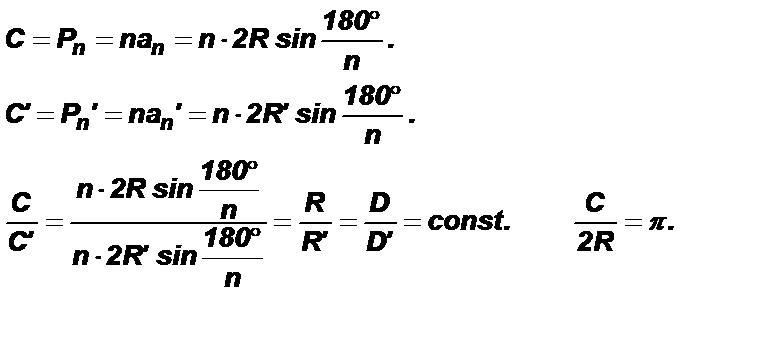

Отношение длины окружности к ее диаметру есть число постоянное для всех окружностей. Из этого соотношения получим формулу для нахождения длины окружности C = 2pR.

Теорема 2 (о длине дуги окружности). Длина дуги окружности определяется по формуле

Так как длина окружности С = 2pR, то длина дуги в 1°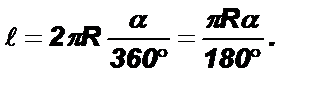

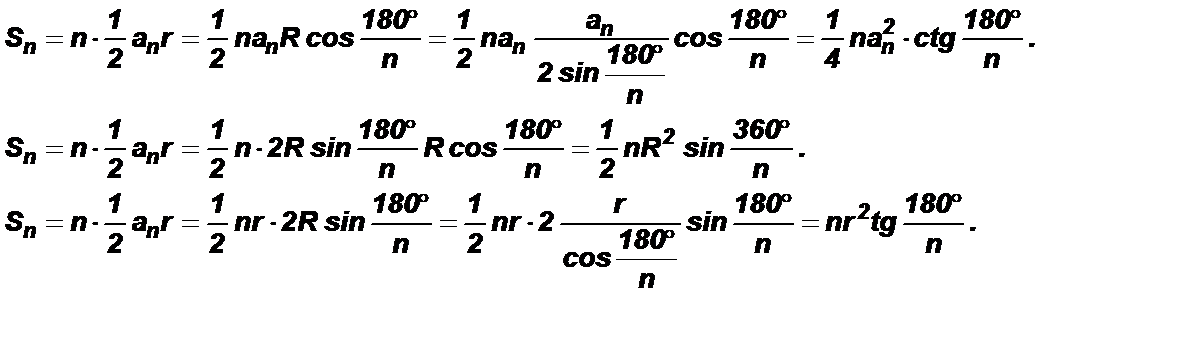
23. Доказать формулу, выражающую площадь правильного многоугольника через его сторону, радиус вписанной и описанной окружностей.

Соединим центр многоугольника с его вершинами. Тогда многоугольник разобьется на n равных треугольников, площадь каждого из которых равна Следовательно,

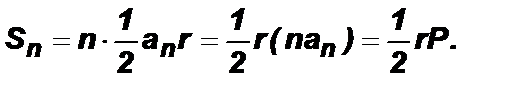
A₂

A₁

О

N₁

Из рассмотрения равнобедренного треугольника получим:

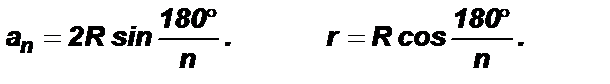
Доказательство:

1) центральный, опирающийся на дугу, стягиваемую хордой А₁А₂;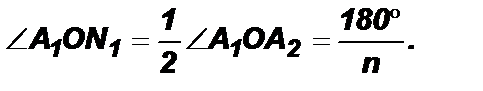

2) Из ∆ А₁ОN₁ (ÐА₁N₁О = 90°):

24. Правильные многоугольники. Доказать теорему о том, что около любого правильного многоугольника можно описать окружность и в любой правильный многоугольник можно вписать окружность.

Определение 1. Многоугольник называется вписанным в окружность, а окружность – описанной около многоугольника, если все вершины многоугольника лежат на окружности.

Теорема 1: Около любого правильного многоугольника можно описать окружность, и притом только одну.

:

Дано: А₁А₂…А_n – правильный многоугольник.

Доказать: 1) существует окружность с центром О, описанная около многоугольника А₁А₂…А_n; 2) эта окружность единственная.

Доказательство:

1) Пусть лучи А₁О и А₂О – биссектрисы углов А₁ и А₂ – пересекаются в точке О. Докажем, что точка О – центр описанной около многоугольника А₁А₂…А_n окружности.

2) Рассмотрим ∆А₁ОА₂ – равнобедренный, т. к. по определению правильного многоугольника Þ по определению биссектрисы Þ Медиана ОN₁, проведенная к основанию равнобедренного треугольника, является высотой треугольника, т. е. серединным перпендикуляром.

3) Рассмотрим ∆А₁ОА₂ и ∆А₂ОА₃.

Из равенства треугольников Þ

4) Аналогично доказывается 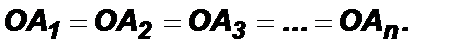След-но, точка О равноудалена от всех вершин правильного многоугольника А₁А₂…А_n и является центром описанной окружности, а радиусом окружности является отрезок ОА₁.

5) Докажем, что эта описанная окружность единственная. Рассмотрим три любые вершины многоугольника, например, 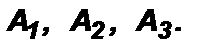Так как через любые три точки, не лежащие на одной прямой, проходит только одна окружность, то около правильного многоугольника А₁А₂…А_n можно описать единственную окружность.

Определение 2. Многоугольник называется описанным около окружности, а окружность – вписанной в многоугольник, если все стороны многоугольника являются касательными к окружности.

Теорема 2: В любой правильный многоугольник можно вписать окружность, и притом только одну.

Дано: А₁А₂…А_n – правильный многоугольник.

Доказать: 1) существует окружность с центром О, вписанная в многоугольник А₁А₂…А_n; 2) эта окружность единственная.

Доказательство:

1) Из доказательства предыдущей теоремы следует, что серединные перпендикуляры Таким образом, окружность радиуса ОN₁ c центром в точке О является вписанной в многоугольник А₁А₂…А_n окружностью.

2) Докажем, что эта вписанная окружность единственная. Предположим, что наряду с рассматриваемой окружностью с центром в точке О и радиусом ОN₁ существует и другая вписанная в многоугольник окружность с центром в точке О₁. Тогда точка О₁ равноудалена от сторон многоугольника и лежит на каждой из биссектрис его углов, а следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. равен ОN₁. Таким образом, вторая окружность совпадает с первой.

Дата добавления: 2015-04-24