Формула, устанавливающая связь между длинами сторон произвольного треугольника и его площадью, называется формулой Герона

Выразить площадь треугольника через его стороны.

Зная стороны треугольника, найти его высоты;

В треугольнике АВС: ВС = а; АВ = с; АС = b; AE ^ BC, AE = h_a; AE∩BC = {E};

CE = x; BE = a─x.

По теореме Пифагора из DСАЕ: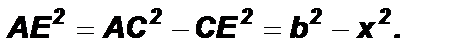

По теореме Пифагора из DВАЕ: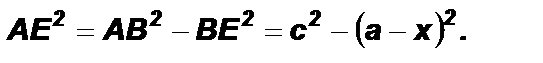

По аналогии запишем:

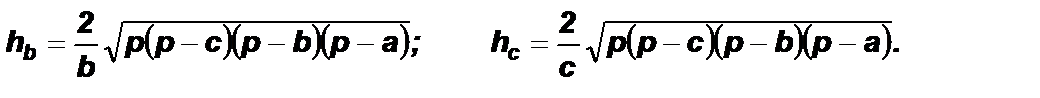
Найдем площадь DАВC:

29. Доказать формулу площади треугольника, выраженную через радиус вписанной окружности.

F

E

D

C

B

A

O

По свойству биссектрисы угла:

AB = c; BC = a; AC = b.

Площадь треугольника ABC:

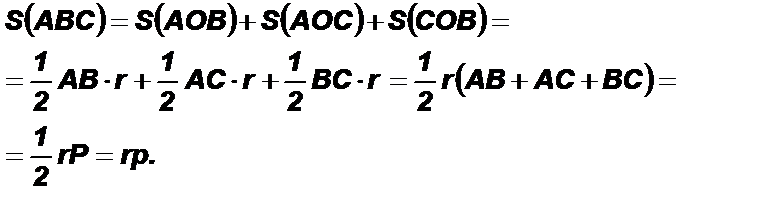
30. Доказать теорему о площади треугольника. Следствие.

Лемма о площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.

Доказательство: Пусть дан прямоугольный треугольник Т со сторонами a и b. Достроим его до прямоугольника Р со сторонами a и b, проведя через вершины его острых углов прямые, перпендикулярные катетам. Гипотенуза треугольника разбивает прямоугольник на два равных треугольника Т и Т₁. Поэтому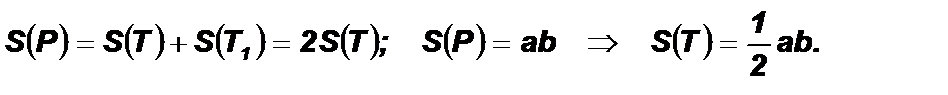

N

C

B

А

N

C

B

А

Теорема о площади произвольного треугольника. Площадь треугольника равна половине произведения любой из его сторон и проведенной к ней высоты:

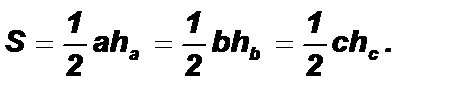
Доказательство:

1) Пусть D АВС – остроугольный, тогда BN ^ AC лежит внутри треугольника.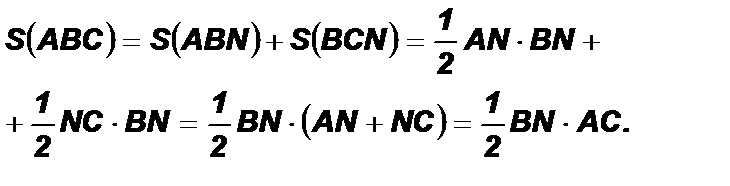

2) Пусть D АВС – тупоугольный с тупым углом С и BN ^ AC лежит внутри треугольника.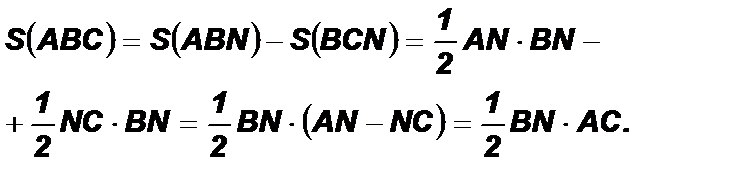

N

C

B

А

Вычисление площади треугольника через угол. Площадь треугольника равна половине произведения его сторон и синуса угла между ними:

Доказательство:

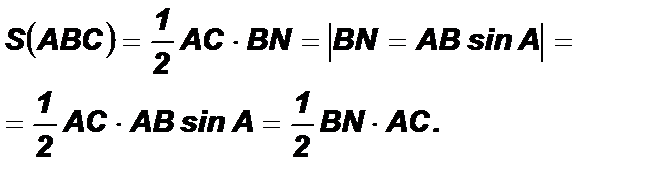
Следствие из теоремы о площади треугольника. Если высоты двух треугольников равны, то их площади относятся как их основания.

Доказательство: Пусть даны треугольники с основаниями a и b и высотой h.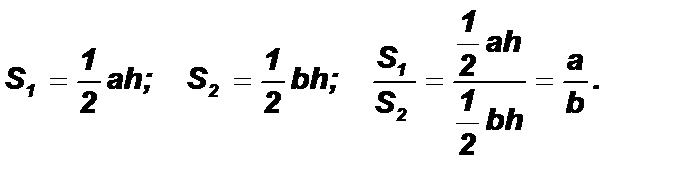

K

H

А₁

C₂

B₂

C₁

B₁

А₁

B₂

C₂

А₂

C₁

B₁

Теорема об отношении площадей треугольников. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:

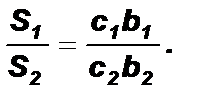
Доказательство:

1. Наложим ∆ А₂В₂С₂ на ∆ А₁В₁С₁ так, чтобы совпали равные углы ÐА₁ = ÐА₂.

2. ∆ А₁В₁С₂ и ∆ А₁В₁С₁ имеют общую высоту В₁Н, следовательно

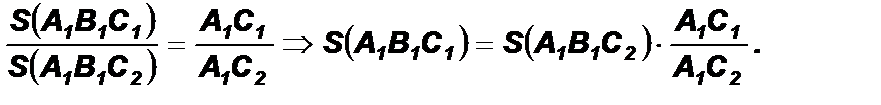3. ∆ А₁В₂С₂ и ∆ А₁В₁С₂ имеют общую высоту С₂К, следовательно

4. Найдем отношение площадей ∆ А₁В₁С₁ и ∆ А₂В₂С₂

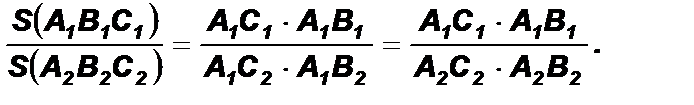
31. Доказать теорему о площади параллелограмма.

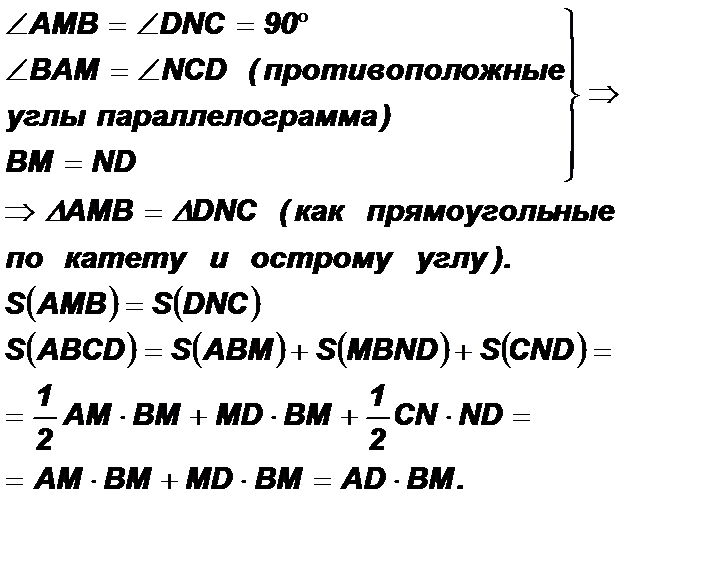
Определение 2. Высотой параллелограмма называется общий перпендикуляр его противоположных сторон (или прямых, содержащих эти стороны).

Теорема о площади параллелограмма 1. Площадь параллелограмма равна произведению его стороны и проведенной к ней высоты: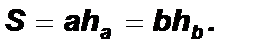

M

N

D

C

B

А

Доказательство:

Теорема о площади параллелограмма 2. Площадь параллелограмма равна произведению его сторон и синуса угла между ними:

D

C

B

А

Доказательство:

32. Доказать теорему о скалярном произведении двух векторов и теорему косинусов с помощью векторов.

Из курса физики известно, что механическая работа А, совершаемая постоянной силой 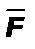при перемещении 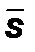тела, равна произведению: где j - угол между направлением перемещения и направлением действия силы. Следует заметить, что механическая работа – скалярная величина.

Проекция вектора на ось с единичным вектором 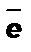вычисляется именно как такое произведение: 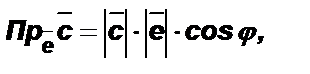где j - угол между векторами и .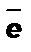

Определение. Скалярным произведением двух ненулевых векторов называется произведение их модулей и косинуса угла между ними.

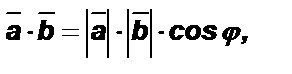где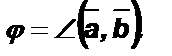

Если один из векторов нулевой, то их скалярное произведение равно 0.

Если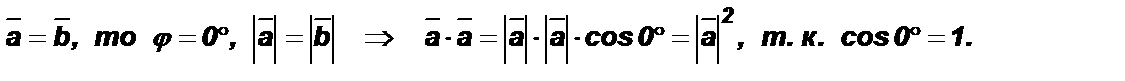

Для любых ненулевых векторов и 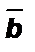их скалярное произведение тогда и только тогда, когда При ненулевых модулях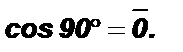

Теорема (о выражении скалярного произведения векторов в координатах). Скалярное произведение векторов равно сумме произведений одноименных координат этих векторов: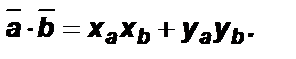

y

О

х

В

А

Доказательство:

Отложим от начала координат вектор 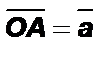и вектор 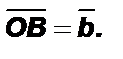Пусть векторы неколлинеарны и образуют 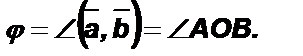Используем обобщенную теорему Пифагора для вычисления длины стороны АВ в ∆ОАВ:

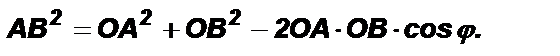
Здесь 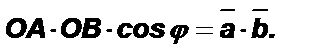Тогда

Выразим полученную формулу в координатах:

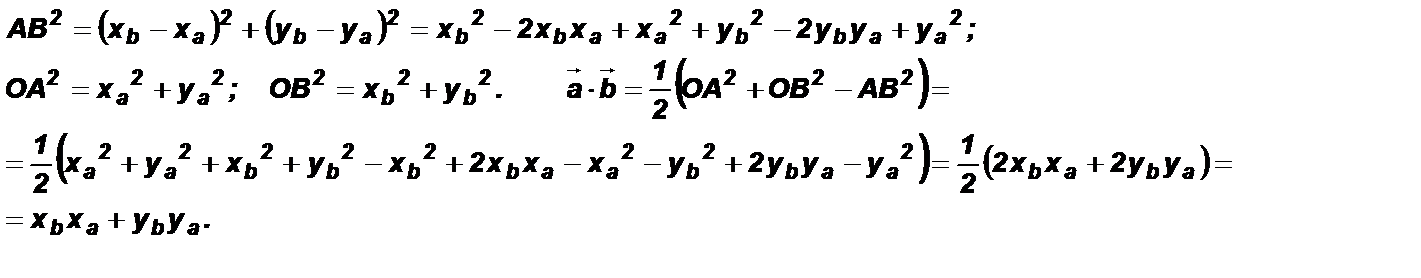
Если векторы и 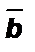коллинеарны, то 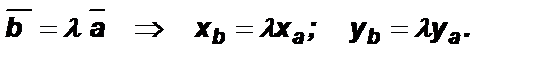Тогда

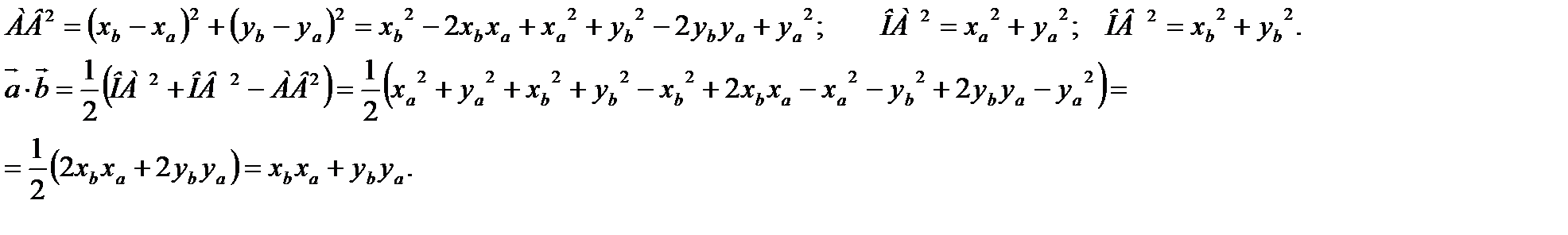Свойства скалярного умножения.

Выполняются для любых векторов 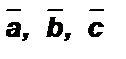и любого числа х:

Доказанные свойства вместе со свойствами сложения векторов позволяют скалярно умножать суммы и разности векторов по правилам алгебры.

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

D

a

C

В

А

Доказательство:

Пусть АВС – данный треугольник. Докажем, что

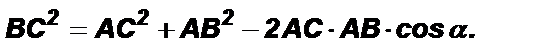
Имеем векторное равенство: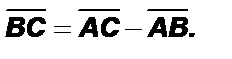

Возведя это равенство скалярно в квадрат, получим: 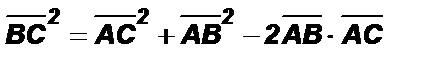или

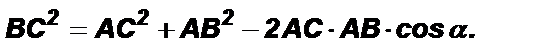
Следствие. Квадрат стороны треугольника равен сумме квадратов двух других сторон «±» удвоенное произведение одной из них на проекцию другой. Знак «+» надо брать, если противолежащий угол тупой, а знак «-», когда угол острый.

33. Доказать теорему синусов. Следствие.

D

С

В

А

Теорема синусов. Отношение двух сторон треугольника равно отношению синусов противолежащих им углов.

Доказательство:

Дата добавления: 2015-04-24