
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение матриц
|
|
|
|
Умножение на число
Сложение матриц
Транспонирование матриц
Равенство матриц
Пусть  ,
,  . Тогда
. Тогда 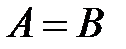

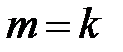 ,
, 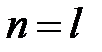 и
и 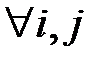
 . То есть матрицы равны, когда число строк, столбцов и каждый элемент одной матрицы равен числу строк, столбцов и каждому элементу другой матрицы соответственно.
. То есть матрицы равны, когда число строк, столбцов и каждый элемент одной матрицы равен числу строк, столбцов и каждому элементу другой матрицы соответственно.
Транспонирование матрицы

это переход к матрице

Пример
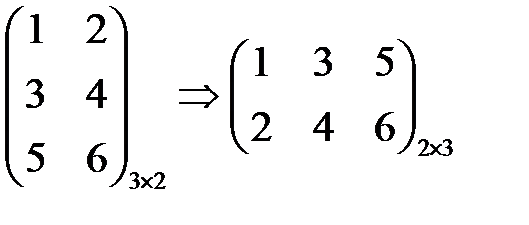
Свойство транспонирования:
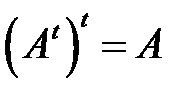
Пусть даны две матрицы
 ;
; 
Тогда их суммой называется матрица
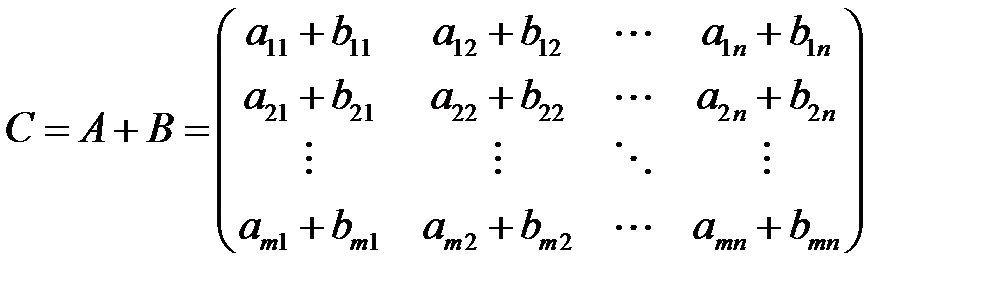
То есть 
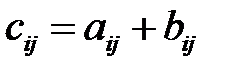 .
.
Пусть дана матрица

Произведением матрицы  на число
на число  является матрица
является матрица

То есть 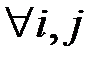
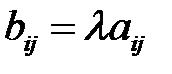 .
.
Пусть даны матрицы  и
и 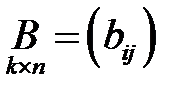 (т.е. число столбцов первой матрицы равно числу строк второй матрицы). Тогда произведением этих матриц называется матрица
(т.е. число столбцов первой матрицы равно числу строк второй матрицы). Тогда произведением этих матриц называется матрица 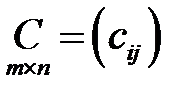 , где
, где
 ,
,
т.е. произведение  -ой строки матрицы
-ой строки матрицы 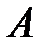 на
на  -ый столбец матрицы
-ый столбец матрицы  .
.
[_]
3. Определители 2-ого и 3-его порядков: их определения и свойства
Пусть дана квадратная матрица порядка 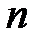 .
.
 :
: 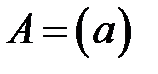
 .
.
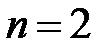 :
: 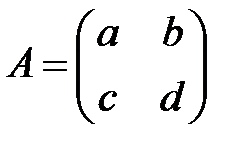
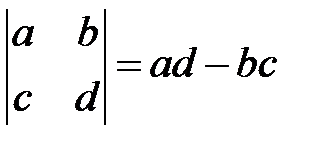 .
.
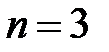 :
: 
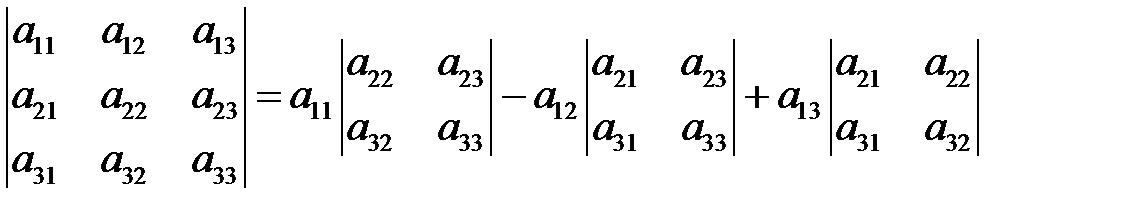
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 503; Нарушение авторских прав?; Мы поможем в написании вашей работы!