
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение. Каноническое уравнение
Плоскость
Свойства
Каноническое уравнение
Определение
Парабола – кривая на плоскости, для каждой точки которой расстояние до некоторой фиксированной точки плоскости 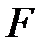 (фокуса параболы) равно расстоянию до некоторой фиксированной прямой (директрисы параболы), которая не проходит через фокус параболы.
(фокуса параболы) равно расстоянию до некоторой фиксированной прямой (директрисы параболы), которая не проходит через фокус параболы.
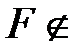 директрисе
директрисе 
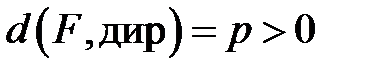 .
.
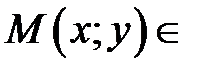 параболе
параболе 
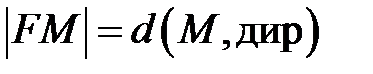

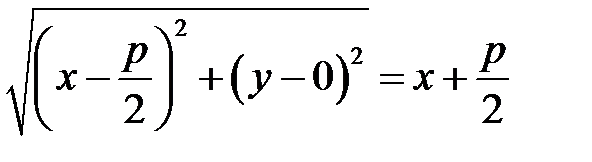
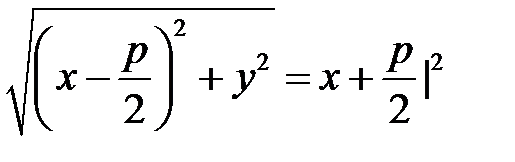
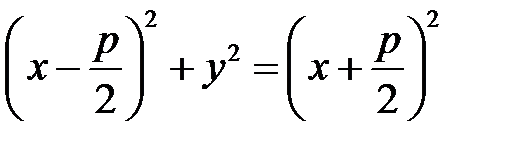
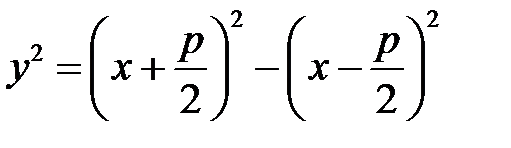

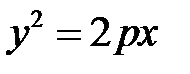 (*)
(*)
1. Парабола симметрична относительно оси 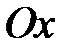 .
.
2. 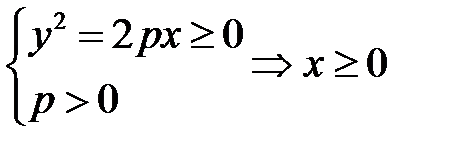 , значит парабола лежит в правой полуплоскости.
, значит парабола лежит в правой полуплоскости.
3. Начало координат (точка 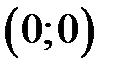 ) принадлежит параболе и является самой левой ее точкой.
) принадлежит параболе и является самой левой ее точкой.
4. Исследуем форму параболы при 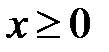 и
и 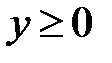 . Из (*)
. Из (*)
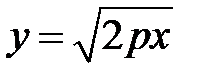
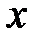 возрастает от
возрастает от 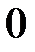 до
до 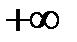 ,
, 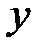 возрастает от
возрастает от 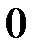 до
до 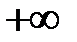 .
.
[_]
Плоскость 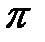 определяется точкой
определяется точкой 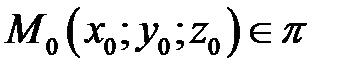 и нормальным вектором
и нормальным вектором 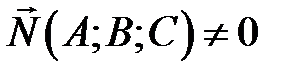 (т.е.
(т.е. 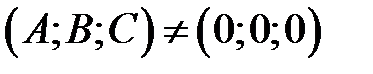 ).
).
Нормальный вектор 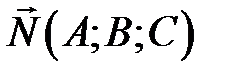 плоскости
плоскости  - любой ненулевой вектор перпендикулярный любому вектору, лежащему в плоскости
- любой ненулевой вектор перпендикулярный любому вектору, лежащему в плоскости 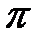 .
.
|
|
Дата добавления: 2015-04-24; Просмотров: 492; Нарушение авторских прав?; Мы поможем в написании вашей работы!