Обработка результатов измерений. Под ошибкой измерения понимается разность между результатом измерений и истинным значением измеряемой величины

Под ошибкой измерения понимается разность между результатом измерений 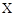и истинным значением измеряемой величины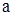 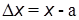. Ошибка измерений обычно неизвестна, так как неизвестно истинное значение измеряемой величины 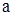. Поэтому важное практическое значение имеет оценка получаемой ошибки и истинного значения.

Нормальный закон распределения ошибок (закон Гаусса) широко распространен в математической статистике. Гауссово распределение описывается следующим выражением . где 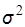- генеральная дисперсия, характеризующая разброс результатов; - плотность распределения, нормированная условием 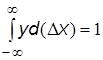, означающим, что вероятность появления ошибки в пределах всей числовой оси равна единице. Графически Гауссово распределение может быть проиллюстрировано рис.3.1, где .

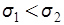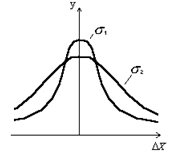Рис. 3.1

Вероятность того, что ошибка находится в интервале [-z, z] определяется площадью криволинейной трапеции (рис.3.2) 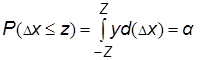, где - интеграл вероятностей.

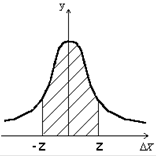Рис. 3.2

Данное выражение означает, что с доверительной вероятностью ошибки измерений находятся в доверительном интервале 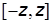. Чем большей надежности мы требуем при определении доверительного интервала, тем он больше и наоборот.

Использование распределения Гаусса на практике довольно затруднительно ввиду сложности определения генеральной дисперсии 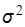по ограниченному количеству повторных опытов. Для оценки ошибок обычно используют другие способы, рассмотрение которых потребует введения следующих основных определений:

среднеарифметическое значение величин ;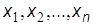

абсолютная погрешность 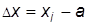или, поскольку неизвестно, ;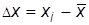

относительная погрешность ;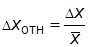

выборочная дисперсия ;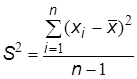

среднеквадратичное отклонение ;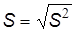

генеральная дисперсия .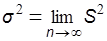

При Гауссовом распределении 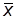является математическим ожиданием истинного значения . Дисперсия среднего 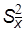при этом связана с дисперсией результатов 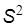соотношением , которое широко известно под названием фундаментальный закон возрастания точности. В соответствии с этим выражением для повышения точности, например в три раза, необходимо увеличить число опытов в девять.

Приведенные соотношения, разумеется, можно использовать только для случая, если ошибки измерений подчиняются нормальному закону распределения. Для качественной проверки близости закона распределения ошибок к нормальному на практике широко используются гистограммы. Для их построения по таблице результатов повторных измерений определяются максимальное и минимальное 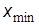значения. Отрезок делится на 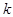равных элементарных отрезков 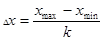, где 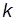выбирается, например, по правилу Штюргеса 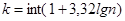, где -операция выделения целого.

После этого подсчитываются количества попаданий результатов измерений в каждый элементарный отрезок 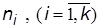, которые далее переводятся в относительные частоты

Гистограммы строят в виде столбиков, основаниями которых являются элементарные отрезки и высотой, равной относительной частоте попаданий результатов в данный отрезок. Часто центры соседних столбиков соединяют отрезками прямых, в результате чего получается ломаная линия, называемая полигоном

Определение доверительного интервала с помощью интеграла вероятностей требует знания генеральной дисперсии . На практике она неизвестна ввиду ограниченного числа повторных опытов, по которым можно определить только эмпирическую дисперсию . Используя эмпирическую дисперсию определить доверительный интервал можно с помощью распределения Стьюдента, имеющего вид 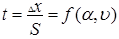, где - доверительный интервал; - доверительная вероятность; - количество степеней свободы. Для одномерных распределений, с которыми мы имеем дело в данном случае, 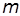=1. С использованием распределения Стьюдента доверительный интервал, в котором лежат все измеряемые значения, определяется выражением .

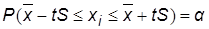Доверительный интервал для истинного значения можно получить, используя фундаментальный закон возрастания точности: .

Проведем статистическую обработку на примере данных табл. 3.3.

Таблица 3.3

Номер опыта i
Результат xi	3,2	2,5	4,1	4,9	3,9	3,7	2,9	3,6	2,9	1,1

Текст документа MathCAD:

Варианты заданий. Произвести статистическую обработку данных. Данные взять из таблицы 3.4.

Таблица 3.4

№ п/п	Результаты измерений xi
	8,579	10,267	7,904	11,042	7,375	15,7	1,822	12,611	16,537	13,255
	13,527	7,086	5,272	11,392	14,423	13,496	7,71	11,528	11,488	7,593
	8,119	8,34	8,962	8,607	10,753	8,88	9,181	13,869	10,582	16,259
	5,313	10,237	11,261	14,882	11,859	4,849	5,882	17,188	12,2	9,992
	7,462	6,948	5,108	6,839	13,348	12,836	12,279	6,815	8,76	14,821
	10,071	9,005	8,631	11,191	11,488	9,763	10,249	11,267	7,684	9,597
	5,611	10,605	15,042	7,277	12,359	9,623	6,647	12,172	10,873	7,355
	4,199	7,122	6,019	8,819	6,974	8,218	12,84	12,414	9,001	4,606
	12,024	1,88	9,27	5,91	7,609	8,177	9,268	10,989	13,402	8,176
	8,164	6,729	8,421	9,079	9,557	7,071	9,147	8,931	6,568	9,714
	9,199	5,393	10,813	11,243	2,208	6,41	7,286	12,461	13,19	7,595
	9,093	9,613	10,537	9,914	8,593	9,257	7,434	10,922	7,457	8,501
	10,179	8,506	10,169	7,54	9,858	9,246	10,058	15,358	9,783	8,592
	13,107	14,174	5,6	13,864	6,502	5,8	8,453	9,465	11,925	9,378
	5,274	9,931	11,102	12,342	14,849	8,17	10,415	6,43	2,211	14,537
	8,636	4,591	5,089	10,682	11,547	7,255	14,92	11,785	13,89	11,451
	6,195	12,979	6,489	9,915	9,027	7,106	4,928	11,045	11,931	9,352
	12,772	9,845	8,89	4,022	7,144	13,243	9,483	9,155	13,362	10,692
	10,099	8,325	11,237	7,987	7,09	12,212	5,175	8,641	8,252	9,144
	11,928		7,568	6,365	8,138	6,724	12,113	10,235	11,548	13,206
	9,887	11,661	14,57	5,056	8,57	10,657	9,273	10,617	12,023	10,693
	8,704	8,771	14,082	7,047	8,882	6,331	8,803	3,867	13,662	6,895
	3,845	6,626	11,578	11,265	8,226	7,943	10,451	2,353	10,678	7,315
	4,839	12,196	4,748	5,223	16,613	10,521	13,667	10,827	12,559	8,259
	14,575	1,382	10,792	8,941	11,773	13,256	9,229	13,407	4,36	16,729
	14,589	10,217	10,316	5,344	6,244	9,582	8,879	13,212	4,211	12,045
	9,194	9,964	11,82	6,253	8,425	10,153	8,941	11,267	5,04	13,343
	4,35	12,492	8,366	14,298	7,61	13,629	12,128	13,072	9,374	13,484
	9,989	13,968	8,731	8,568	6,79	5,885	12,53	10,829	12,146	10,891
	10,368	0,629	5,057	9,583	5,146	8,696	9,052	7,472	4,908	11,429

Дата добавления: 2015-05-08