Аппроксимация функций

Одним из распространенных и практически важных случаев связи между аргументом и функцией является задание этой связи в виде некоторой таблицы { x_i; y_i }, например, экспериментальные данные. На практике часто приходится использовать табличные данные для приближенного вычисления у при любом значении аргумента х (из некоторой области). Этой цели служит задача о приближении (аппроксимации) функций: данную функцию f (x) требуется приближенно заменить некоторой функцией g (х) так, чтобы отклонение g (х) от f (x) в заданной области было наименьшим. Функция g (х) при этом называется аппроксимирующей. Если приближение строится на заданном дискретном множестве точек { x_i }, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др.

Пример. Используя линейную аппроксимацию получить эмпирическую формулу для функции у = f (x), заданной в табличном виде:

xi	0.75	1.50	2.25	3.00	3.75
yi	2.50	1.20	1.12	2.25	4.28

Текст документа MathCAD.

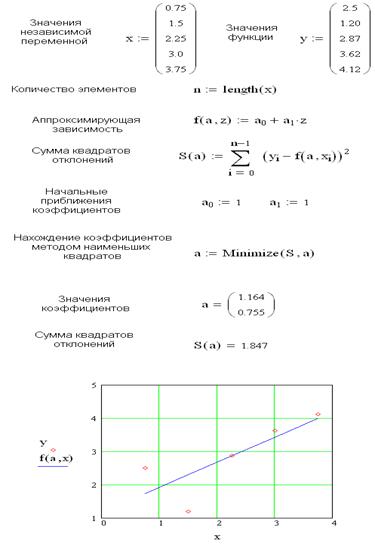
Сумма квадратов отклонений указывает на статистическую оценку среднеквадратической погрешности. Чем она меньше, тем точнее полученная аппроксимирующая функция у = g (х). Для зависимости в виде полинома второй степени необходимо изменить выражение для аппроксимирующей зависимости и добавить начальное приближение для коэффициента a₂.

Варианты заданий. Получить эмпирические формулы в виде полиномов первой и второй степени и оценить их погрешность для функции у = f (x), заданной таблично. Данные взять из таблицы 3.5.

Таблица 3.5

1.	xi	-3	-2	-1
yi	-0.71	-0.01	0.51	0.82	0.88	0.51	0.49
2.	xi	-6.6	-5.38	-3.25	-1.76	2.21	3.6	4.5
yi	2.89	1.41	0.29	-0.41	-0.69	-0.7	1.2
3.	xi
yi	-0.31	0.9	2.11	3.3	4.51	5.73	6.93
4.	xi	-2	-1
yi	7.1	3.9	1.1	0.8	3.1	4.5	5.3
5.	xi	-2	-1	-0.5		1.5		3.5
yi	5.9	2.8	2.1	3.2	6.1	7.6	4.3
6.	xi	-3	-2	-1
yi	3.1	0.9	0.9	2.8	7.1	6.5	4.1
7.	xi
yi	10.0	7.5	5.5	4.0	3.0	2.0	2.24
8.	xi	-2	-1		1.5	2.3	2.6	2.9
yi	4.2	5.6	6.8	7.2	9.4	10.5	11.8
9.	xi	10.0	12.0	13.0	15.0	18.0	20.0	21.0
yi	0.66	0.89	1.24	1.36	1.56	1.76	1.92
10.	xi	22.0	24.0	27.0	30.0	31.0	35.0	40.0
yi	1.24	1.37	1.46	1.26	1.66	1.84	1.99
11.	xi	-7.0	-6.0	-5.0	-4.0	-3.0	-2.0	-1.0
yi	22.6	24.7	25.6	24.6	23.5	21.8	19.3
12.	xi	-25.0	-23.0	-21.0	-18.0	-17.2	-15.4	-14.0
yi	0.76	0.74	0.61	0.58	0.84	0.92	1.22
13.	xi	-4.0	-3.0	-2.0	-1.0	0.0	1.0	2.0
yi	1.71	1.56	1.24	1.36	1.78	2.21	4.31
14.	xi	-22.0	-20.0	-18.0	-16.0	-14.0	-12.0	-10.0
yi	-2.26	-1.84	-1.92	-1.76	-1.56	-1.64	-1.34
15.	xi	23.0	24.0	25.0	26.0	27.0	28.0	29.0
yi	1.26	1.37	1.44	1.56	1.15	1.28	1.06
16.	xi	30.0	33.0	35.0	37.0	39.0	41.0	43.0
yi	-2.6	-3.7	-2.5	-4.3	-2.3	-5.6	-1.9
17.	xi	44.0	45.0	46.0	47.0	48.0	49.0	50.0
yi	2.24	3.46	5.36	1.89	1.76	1.54	2.12
18.	xi	52.0	54.0	56.0	58.0	60.0	62.0	64.0
yi	-1.28	-1.33	-1.44	-1.67	-1.77	-2.81	-2.16
19.	xi	2.2	2.6	3.0	3.4	3.8	4.2	4.6
yi	1.88	1.65	1.61	1.73	1.56	1.24	1.99
20.	xi	5.1	5.3	5.5	5.7	5.9	6.1	6.3
yi	-2.8	-3.6	-5.7	-3.4	-1.9	-1.7	-1.5
21.	xi	7.15	7.35	7.55	7.75	7.95	8.15	8.35
yi	-2.2	-3.6	-1.7	-2.8	-1.6	-4.5	-2.2
22.	xi	9.1	9.2	9.3	9.4	9.5	9.6	9.7
yi	1.48	1.16	2.08	1.96	1.81	2.31	5.61
23.	xi	-10.2	-10.1	-10.0	-9.9	-9.8	-9.7	-9.6
yi	-6.5	-7.8	-10.2	-5.4	-4.6	-9.5	-10.3
24.	xi	11.0	14.0	17.0	20.0	23.0	26.0	29.0
yi	1.2	1.6	1.9	1.1	1.16	1.24	1.36
25.	xi	-50.0	-48.0	-46.0	-44.0	-42.0	-40.0	-38.0
yi	1.23	1.32	1.57	1.19	1.16	1.10	2.28
26.	xi	-36.0	-34.0	-32.0	-30.0	-28.0	-26.0	-24.0
yi	1.1	1.3	2.1	1.9	1.7	1.5	1.8
27.	xi	21.0	23.0	24.0	28.0	31.0	32.0	36.0
yi	1.24	1.37	1.56	1.64	1.84	1.26	1.14
28.	xi	10.0	13.0	17.0	22.0	28.0	35.0	43.0
yi	1.21	1.36	1.51	1.84	1.06	1.21	1.36
29.	xi	-1.0	0.0	3.0	5.0	8.0	12.0	15.0
yi	-2.1	-3.6	1.2	-4.3	1.8	2.6	-0.2
30.	xi	-8.0	-7.0	-5.0	-3.0	-1.0	2.0	5.0
yi	1.36	1.88	2.45	-2.1	-10.2	-4.4	1.16

Дата добавления: 2015-05-08