Численное решение оптимизационных задач

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют определить наилучший вариант конструкции, наилучшее распределение ресурсов, минимальный урон природной среде и т. п. В процессе решения задачи оптимизации необходимо найти оптимальные значения некоторых параметров (их называют проектными). Выбор оптимального решения проводится с помощью некоторой функции, называемой целевой. Целевую функцию можно записать в виде

, (3.10)

где х ₁, х ₂, …, х_п – проектные параметры.

Можно выделить 2 типа задач оптимизации – безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума функции (3.10) от п действительных переменных и определении соответствующих значений аргументов на некотором множестве G n -мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный. Условные задачи оптимизации – это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве G.

Для поиска экстремумов в MathCad имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.

- Minimize (f, xi,...,х_м) - вектор значений аргументов, при которых функция f достигает минимума;

- Maximize (f, xi,...,х_м) - вектор значений аргументов, при которых функция f достигает максимума; f(xi,...,х_м,...)-функция; xi,...,х_м- аргументы, по которым производится минимизация(максимизация). Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения

Пример. Найти минимальное значение функции одной переменной

f (x) = 24 – 2 x /3 + x ²/ 30 на отрезке [5; 20].

Текст документа MathCAD

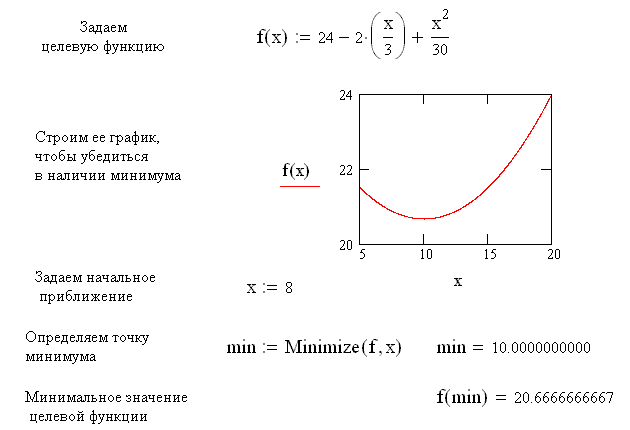
Варианты заданий. Найти координату и минимальное значение функции f (x) на [ a; b ]. Данные взять из таблицы 3.9.

Таблица 3.9

№ п/п	Функция f (x)	Отрезок [a; b]
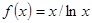
		[1.2; 4]
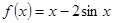
		[0; p/2]
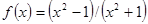
		[-2; 2]
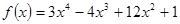
		[-2; 2]
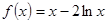
		[1; 3]
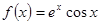
		[p; 3p/2]
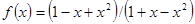
		[0; 1]
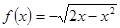
		[0; 2]
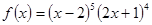
		[-0.5; 1.5]
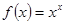
		[0,1; 1.0]
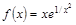
		[1.0; 2,5]
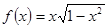
		[-1.0; 0]
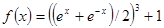
		[-0.5; 0.5]
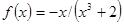
		[0.5; 1.5]
		[1.6; 2.2]
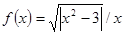
		[1; 2]
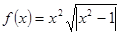
		[0.8; 1.2]
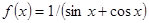
		[0; p/3]
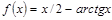
		[0.5; 1.2]
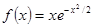
		[-1.5; -0.5]
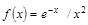
		[-2.0; -1.0]
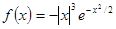
		[-3.0; -1.0]
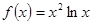
		[0.1; 1.0]
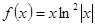
		[-0,05; -0.2]
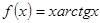
		[-0.5; 0.5]
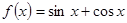
		[p; 3p/2]
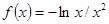
		[1.0; 2.0]
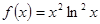
		[0.1; 0.5]
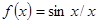
		[p; 2p]
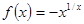
		[2.0; 3.0]

Поиск минимума функций нескольких переменных

Данная задача значительно сложнее первой. Для минимизации функций нескольких переменных Mathcad использует различные методы (сопряженных градиентов, Ньютона и пр.), выбор которых обычно реализуется автоматически самой системой Mathcad.

Пример. Найти координаты и значение минимума функции двух переменных f (x, y) = 100(y – x ²)² + (1– x ²)², если начальная точка поиска имеет координаты М₀ (2; 2). Анализ функции показывает, что min f = 0, x = 1,y=1.

Текст документа MathCAD

Варианты заданий. Найти и вывести на печать координаты и минимальное значение функции двух переменных при погрешностях 10^-2, 10^-5, 10^-20. Поиск начать с точки М₀ (х ₀, у ₀). Данные взять из таблицы 3.10.

Таблица 3.10

№ п/п	Функция f (x, у)	Координаты начальной точки М0 (х 0, у 0).
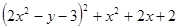
		(1; 1)
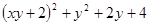
		(2; 2)
		(2; 2)
		(2; 2)
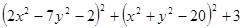
		(2; 2)
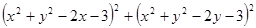
		(2; 2)
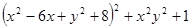
		(2; 2)
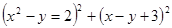
		(2; 2)
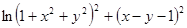
		(2; 2)
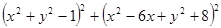
		(2; 2)
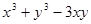
		(0.5; 0.5)
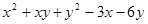
		(0.5; 3.5)
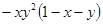
		(0; 0)
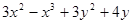
		(0.1; -1.0)
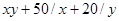
		(4; 1)
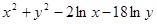
		(0.5; 2.5)
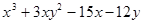
		(1.5; 0.5)
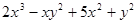
		(0.5; 0.5)
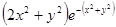
		(0.3; 0.3)
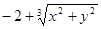
		(0.25; 0.25)
		(0.5; 1.5)
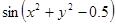
		(0.5; 0.5)
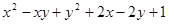
		(-1.5; 0.5)
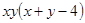
		(1.0; 1.0)
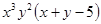
		(2.0; 1.5)
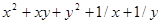
		(0.2; 0.3)
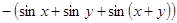
		(p/4; p/4)
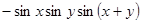
		(p/4; p/4)
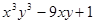
		(2.5; 2.5)
		(1.0; -1.0)

Содержание

1. Содержание и объем курсовой работы……………………………………….

2.Основные приемы работы в системе MathCAD……………………………….

3. MathCAD в инженерно-строительных задачах………………………………

3.1. Табулирование функций……………………………………………

3.2. Решение систем линейных алгебраических уравнений ………….

3.3 Обработка результатов измерений………………………………….

3.4. Аппроксимация функций…………………………………………….

3.5. Численное решение обыкновенных дифференциальных

уравнений………………………………………………………………

3.6. Приближенное вычисление определенных интегралов…………...

3.7. Численное решение нелинейных уравнений……………………….

3.8. Численное решение оптимизационных задач……………………...

Литература

Приложение 1. Системные переменные

p = 3.14159	Число p. Чтобы напечатать нажмите [Ctrl-Shift-P]
e = 2.71828	Основание натурального логарифма
I	Мнимая единица
J	Мнимая единица
TOL=10^-3	Допустимая погрешность при различных ал‑ горитмах (интегрирования, решения уравнений). Изменить значение системной переменной TOL и ниже следующих можно с помощью команды МатематикаÞПараметры.
CTOL=10^-3	Устанавливает точность ограничений в ре‑ шающем блоке, чтобы решение было допус‑ тимым.
ORIGIN=0	Определяет индекс первого элемента векторов и матриц.
FRAME =0	Используется в качестве счетчика при созда‑ нии анимаций.
PRNPRECISION = 4	Число значащих цифр.
PRNCOLWIDTH = 8	Число позиций для числа.
CWD	Текущий рабочий каталог в форме строки.

Приложение 2. Встроенные функции

Дата добавления: 2015-05-08