Приближенное вычисление определенных интегралов

К вычислениям определенных интегралов сводятся многие практические задачи физики, химии, экологии, механики и других естественных наук. На практике формулой Ньютона-Лейбница далеко не всегда удается воспользоваться. В этом случае используются методы численного интегрирования. Обычно они основаны на следующих соображениях: с геометрической точки зрения определенный интеграл представляет собой площадь криволинейной трапеции. Идея многих методов численного интегрирования сводится к разбиению интервала [ a; b ] на множество элементарных участков и нахождению искомой площади как совокупности элементарных площадей, полученных на каждом участке. В зависимости от использованной аппроксимации получаются различные формулы численного интегрирования, имеющие различную точность. Рассмотрим методы трапеций и Симпсона (парабол).

Метод трапеций.

В нем используется линейная интерполяция, т. е. график функции y = f (x) представляется в виде ломаной, соединяющей точки y_i. Формула метода трапеций при постоянном шаге , где п – число элементарных отрезков, имеет вид

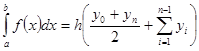. (3.8)

Метод Симпсона

Если подынтегральную функцию заменить отрезками парабол, то формула Симпсона с постоянным шагом интегрирования имеет вид

, где п – четное число (3.9)

Пример. Вычислить методами трапеций и Симпсона значения интеграла

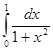
Текст документа MathCAD.

Варианты заданий. Вычислить и вывести на экран значения определенного интеграла средствами MathCad, а также методами трапеций и Симпсона при n=10,50,250. Данные взять из таблицы 3.7. Оценить влияние количества элементарных отрезков на точность интегрирования.

Таблица 3.7

№ п/п	Подынтегральная функция f(x)	Интервал интегрирования [a; b]
		[1; 3.5]
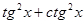
		[p/6; p/3]
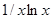
		[1.5; 3.]
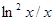
		[1.0; 4,0]
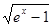
		[0; ln2]
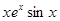
		[1.0; 4.0]
		[0.0; 2.0]
		[2.0; 5.0]
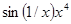
		[1.0; 2.5]
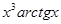
		[0.0; ]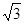
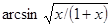
		[0.0; 3,0]
		[1.5; 3.0]
		[0,0; 5.0]
		[2.3; 6.0]
		[0.0; 1.5]
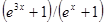
		[0.0; 2.0]
		[0.0; 2.0]
		[0.0; p/4]
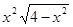
		[0.0; 1.8]
		[0.0; p]
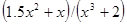
		[0.0; 1.2]
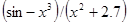
		[2.0; 4.4]
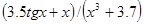
		[0.0; 1.2]
		[2.0; 4.4]
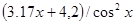
		[1.0; 2.2]
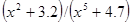
		[0,0; 1.8]
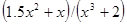
		[0.0; 1.2]
		[1.0; 3.0]
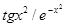
		[0.0; 1.0]
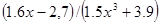
		[1.0; 2.2]

Дата добавления: 2015-05-08