Уравнений

Численное решение обыкновенных дифференциальных

Многие задачи физики, химии, экологии, строительной механики и других разделов науки и техники при их математическом моделировании сводятся к дифференциальным уравнениям. Поэтому решение дифференциальных уравнений является одной из важнейших математических задач.

Среди множества численных методов решения дифференциальных уравнений наиболее простые – это явные одношаговые методы. К ним относятся методы Рунге-Кутта различных порядков.

Требуется найти функцию у = у (х), удовлетворяющую уравнению

(3.3)

и принимающую при х = х ₀ заданное значение у ₀:

. (3.4)

При этом решение необходимо получить в интервале х ₀ £ х £ х _к. Из теории дифференциальных уравнений известно, что решение у (х) задачи Коши (3.3), (3.4) существует, единственно и является гладкой функцией, если правая часть F (x, y) удовлетворяет некоторым условиям гладкости. Численное решение задачи Коши методом Рунге-Кутта 4-го порядка заключается в следующем. На заданном интервале [ х ₀, х _к] выбираются узловые точки. Значение решения в нулевой точке известно у (х ₀) = у ₀. В следующей точке у (х ₁) определяется по формуле

, (3.5)

здесь

(3.6)

т. е. данный вариант метода Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения (3.3). Mathcad располагает обширным набором функций, позволяющих успешно решать обыкновенные дифференциальные уравнения и их системы.

Пример. Решить задачу Коши

. (3.7)

Точное решение .

Выполним решение данной задачи с помощью функции Odesolve.

Текст документа MathCAD.

Как следует из результатов численное решение практически совпадает с точным.

Варианты заданий. Построить графики и вывести в виде таблицы приближенное решение задачи Коши на интервале [0; 1] с помощью функции Odesolve при количестве шагов N=10. Данные взять из таблицы 3.6.

Таблица 3.6

№ п/п	F(x,y)	Y0
1.		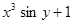0.0
2.		0.1
3.		2.0
4.		0.3
5.		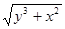0.4
6.		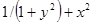0.0
7.		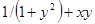0.1
8.		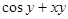0.2
9.		0.3
10.		0.4
11.		0.5
12.		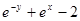0.0
13.		0.5
14.		0.4
15.		0.3
16.		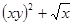0.2
17.		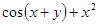0.1
18.		0.0
19.		0.1
20.		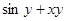0.2
21.		0.3
22.		0.4
23.		0.5
24.		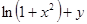0.6
25.		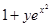0.7
26.		0.0
27.		0.1
28.		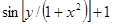0.2
29.		0.3
30.		0.4

Дата добавления: 2015-05-08