Пример 1

Рассмотрим задачу Коши для уравнения

y¹=y, y(0) = 1, (10.17)

точное решение которого есть у(х)=е^х. Рассмотрим сетку 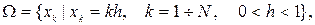c шагом h. Из (10.17) по методу Эйлера следует разностное уравнений .

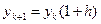Его точное решение имеет вид 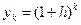. Так как h > 0, то это выражение растет.

Рассмотрим возмущенную задачу Коши (10.17):

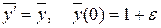, где ε – бесконечно малая величина. Тогда решение имеет вид .

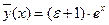Вычислим разность 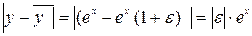. Показательная функция растет быстро, и малая константа не может его ограничить. Таким образом, это решение неустойчивое. Более подробно вопросы устойчивости обсуждаются в следующих разделах.

Очень медленная сходимость при уменьшении h, которая характерна для методов первого порядка, служит препятствием для их использования. Значительная часть остального материала этого раздела посвящена изучению других методов, погрешность которых при стремлении h к нулю убывает с более высокой скоростью. В качестве примера построения одного из таких методов мы рассмотрим модифицированный метод Эйлера, определяемый формулой

y_к+1=y_к+h f(x_к+1, y_к+h f(x_k, y_k)). (10.18)

Обратите внимание на то, что функцию f(x_k,, y_k) в методе Эйлера y_k+1 = y_k+ h f (x_k, y_k) просто заменили на f (x_k, y_k+h f (x_k, y_k)).

Метод Эйлера известен также как метод Рунге-Кутта второго порядка и имеет локальную ошибку дискретизации O(h²). Наиболее распространенным методом Рунге-Кутта является классический метод четвертого порядка, задаваемый формулой

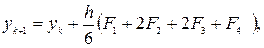(10.19)

где

F₁=f(x_k, y_k), F₂=f(x_k + ),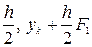

.

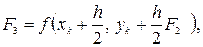
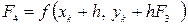Здесь f(x_k, y_k) в отличие от метода Эйлера заменено на взвешенное среднее значение f, вычисленное в четырех различных точках.

В следующем разделе будут рассмотрены методы, которые используют информацию, полученную не только на одном предыдущем шаге, а на многих (не только y _k, но и y _k-1, y _k-2 и т.д.). В настоящем разделе мы имеем дело с методами, зависящими только от y_k и не использующими никаких предыдущих значений. Такие методы называются одношаговыми и могут быть представлены в общем виде как

y_k+1 = y_k+h 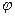(x_k, y_k) (10.20)

с соответствующей функцией φ. В случае метода Эйлера функцией φ является сама f, в то время как для метода обобщающего модифицированный метод Эйлера функция φ имеет вид

φ(x,y)= 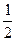[ f(x, y) + f(x+h, y+h f (x,y))]. (10.21)

Метод Рунге-Кутта четвертого порядка (10.19) тоже является одношаговым, и соответствующая функция φ может быть записана в виде аналогичном (10.21).

Для любого одношагового метода (10.21) определим локальную ошибку дискретизации аналогично методу Эйлера соотношением

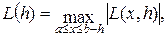(10.22)

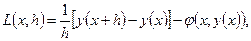
где, как и раньше y(x) - точное решение дифференциального уравнения.

Если для данной функции φ окажется, что L(h) = o(h^p) при некотором целом p, то при соответствующих предположениях относительно функций φ и f можно показать, что глобальная ошибка дискретизации будет также порядка р по h, т.е.

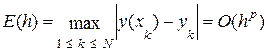. (10.23)

Порядок метода (10.20) определяется как целое р, для которого L(h) = О(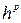). Такое определение порядка является некоторым утверждением о свойствах самого метода. При этом предполагается, что решение дифференциального уравнения у имеет ограниченные производные до определенного порядка. Например, для метода Эйлера мы показали, что р=1 в предположении (10.10). Как будет продемонстрировано ниже, для других методов может потребоваться ограниченность производных решения и функции f более высокого порядка.

Сравнительно несложно показать, что локальная ошибка дискретизации модифицированного метода Эйлера есть О(h²), но мы получим это как следствие более общего анализа, который служит основанием для методов Рунге-Кутта.

Здесь можно пояснить следующее: в методе Эйлера мы ориентируемся по касательной к графику функции в данной точке и получаем ошибку O(h). Если подобрать коэффициенты рядов Тейлора, подправить их так, чтобы получилась секущая графика функции, проходящая через данную точку, то ошибка будет меньше. Давайте рассмотрим функцию φ, определяемую соотношением

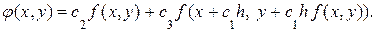
Мы хотим выбрать константы с₁, с₂ и с₃ так, чтобы максимизировать порядок одношагового метода (10.20). Т.е. хотим найти наилучшую определяемую константами с₂ и с₃ линейную комбинацию двух значений f, и найти в какой точке интервала при этом следует вычислять второе значение f, что задается константой с_{1 .}

Разложим функцию φ в ряд Тейлора по двум переменным в окрестности точки (x, y).

Разлагая сначала по переменной х, получаем

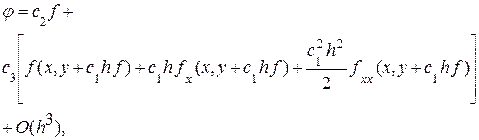
где f(x, y) обозначено через f, а частные производные по х - через f_x и f_xx. Воспользовавшись теперь разложением по y, где все встречающиеся частные производные вычислены в точке (x, y), имеем

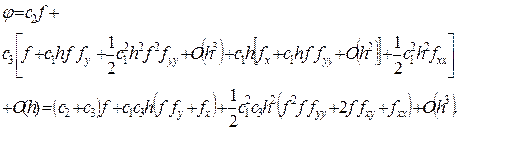
(10.24)

С другой стороны, для точного решения дифференциального уравнения y(x) имеем

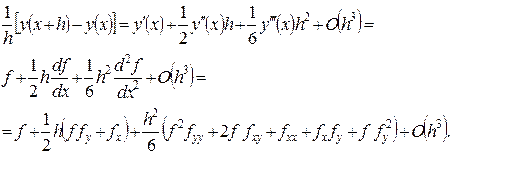(10.25)

Объединяя теперь (10.24) и (10.25), получаем

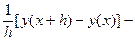φ(x, y(x(x)) =

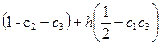(f f_y+f_x)+

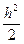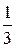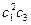+ ( - ) (f²f_yy+2ff_xy+f_xx)+ 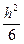(f_x f_y+ 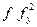)+О(h³). (10.26)

Если мы потребуем, чтобы

с₂ + с₃ = 1, с₁с₃ = ½, (10.27)

то первые два члена в (10.27) обратятся в нуль для любой функции f. Однако член 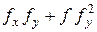в общем случае не будет тождественно равен нулю. Так что, как бы мы ни выбирали константы, самое большое, что мы можем иметь

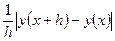– φ (x, y(x)) = О(h²), (10.28)

что и будет выполняться всякий раз, когда удовлетворены условия (10.28) и все необходимые производные ограничены. Таким образом, L(h) = О(h²) и все методы, выделенные условием (10.28), имеют второй порядок.

Дата добавления: 2015-05-26