Многошаговые методы

Конспект помогли составить: В.А. Зайцева, В.В. Лакота, Е.В. Чернавская, Ю.Р. Шабаева.

Вернемся теперь к задаче Коши:

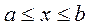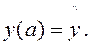, (11.1)

В методах Эйлера и Рунге-Кутта в предыдущем разделе значение зависело только от информации в предыдущей точке .

Кажется вполне вероятным, что можно добиться большей точности, если использовать информацию о нескольких предыдущих точках , , …. Именно так и поступают в многошаговых методах.

Большой и важный класс многошаговых методов возникает на основе следующего подхода. Если подставить в (11.1) точное решение 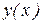и проинтегрировать это уравнение на отрезке , то получим

, (11.2)

где в последнем члене предполагаем, что р(х) – полином, аппроксимирующий 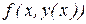. Чтобы построить этот полином, предположим, как обычно, что - приближения к решению в точках . По-прежнему считаем, что узлы 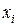расположены равномерно с шагом h. Тогда 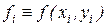(i=k, k - 1,..., k - N) есть приближения к 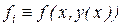в точках . В качестве р возьмем интерполяционный полином для набора данных 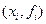(i=k, k - 1,..., k - N). Таким образом, р – полином степени N, удовлетворяющий условиям (i=k, k - 1,..., k - N). В принципе можем проинтегрировать этот полином явно, что ведет к следующему методу:

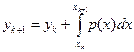. (11.3)

В простейшем случае, когда N=0, полином р есть константа, равная 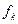, а (19.3) превращается в обычный метод Эйлера. Если N=1, то р есть линейная функция, проходящая через точк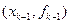и и 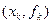, т.е.

.

Интегрируя этот полином от до 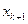, получаем следующий метод:

, (11.4)

который является двухшаговым, поскольку использует информацию в двух точках и . Аналогично, если N=2, то р есть квадратичный полином, интерполирующий данные 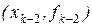, и 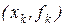, а соответствующий метод имеет вид

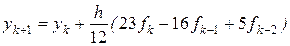. (11.5)

Если , то интерполяционный полином является кубическим, а соответствующий метод определяется формулой

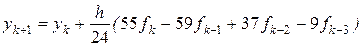. (11.6)

Отметим, что метод (19.5) является трехшаговым, а (11.6) – четырехшаговым.

Формулы (11.4) – (11.6) известны как методы Адамса-Башфорта. Метод (11.4) имеет второй порядок точности, поэтому его называют методом Адамса-Башфорта второго порядка. Аналогично методы (11.5) и (11.6) называют соответственно методами Адамса-Башфорта третьего и четвертого порядков. Продолжая этот процесс, и используя все большее число предыдущих точек, а следовательно, получая интерполяционный полином 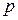более высокой степени, мы получим методы Адамса-Башфорта сколь угодно высокого порядка. При этом с ростом 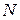формулы становятся все более громоздкими, но принцип остается тем же.

Многошаговые методы порождают проблему, которая не возникала при использовании одношаговых методов. Эта проблема становится понятной, если, например, рассмотреть метод Адамса-Башфорта четвертого порядка (11.6). Нам задано начальное значение , но при 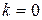для счета по формуле (11.6) необходима информация в точках 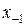, 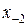и , которая, естественно, отсутствует. Сложность заключается в том, что многошаговые методы в начале работы нуждаются в помощи. Мы не можем использовать (11.6) при или (11.5) при . Обычный выход из положения состоит в использовании какого-либо одношагового метода того же порядка точности, например, метода Рунге-Кутта, до тех пор, пока не будет получено достаточно значений для работы многошагового метода. Или же можно на первом шаге использовать одношаговый метод, на втором – двухшаговый и так далее, пока не будет получено достаточно значений. При этом, однако, существенно, чтобы эти стартовые значения были вычислены с той же степенью точности, с какой будет работать окончательный метод. Так как стартовые методы обычно имеют более низкий порядок, вначале приходится считать с меньшим шагом и использовать больше промежуточных точек.

Методы Адамса-Башфорта используют уже сосчитанные значения в точке 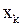и в предыдущих точках. В принципе при построении интерполяционного полинома мы можем использовать и точки , и т.д. Простейший случай при этом состоит в использовании точек 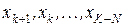и построении интерполяционного полинома степени , удовлетворяющего условиям . При этом возникает класс методов, известных как методы Адамса-Моултона. 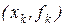Если , то p – линейная функция, проходящая через точки и , и соответствующий метод

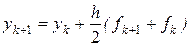(11.7)

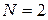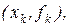
является методом Адамса-Моултона второго порядка. Если , то - кубический полином, построенный по точкам и и 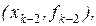соответствующий метод

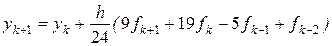(11.8)

является методом Адамса-Моултона четвертого порядка.

Заметим теперь, что в формулах (11.7) и (11.8) значение неизвестно. Дело в том, что для вычисления нужно знать значение 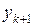, которое само пока является неизвестным. Следовательно, методы Адамса-Моултона определяют 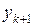только неявно. Так, например, соотношение (11.7) является уравнением

(11.9)

относительно неизвестного значения 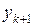. То же самое справедливо и для метода (11.8). Поэтому методы Адамса-Моултона называются неявными. В то же время методы Адамса-Башфорта называют явными, поскольку они для нахождения значения 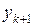не требуют решения никаких уравнений.

На практике обычно не решают непосредственно уравнение (11.9), а используют совместно явную и неявную формулы, что приводит к методу прогноза и коррекции. Одним из широко используемых методов прогноза и коррекции является объединение методов Адамса четвертого порядка (11.6) и (11.8):

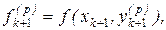(11.10)

.

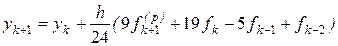Обратите внимание на то, что в целом этот метод является явным. Сначала по формуле Адамса-Башфорта вычисляется значение , являющееся «прогнозом» для 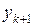. Затем используется для вычисления приближенного значения , которое в свою очередь используется в формуле Адамса-Моултона. Таким образом, формула Адамса-Моултона «корректирует» приближение, даваемое формулой Адамса-Башфорта.

Дата добавления: 2015-05-26