Метод стрельбы

Конспект помогли составить А. Батсайхан, В.С. Мищевская.

Метод стрельбы идейно прост, но он может страдать от неустойчивости, возникающей при решении задачи Коши.

Проиллюстрируем метод стрельбы на примере.

Рассмотрим уравнение

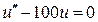(14.1)

с граничными условиям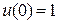и и .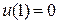

Составим характеристическое уравнение и найдем его корни:

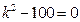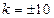, . (14.2)

Точным решением этой краевой задачи является функция

.

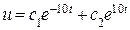Находим постоянные из краевого условия (14.1):

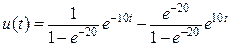_. (14.3)

Получим это решение методом стрельбы и сравним с (14.3). Делаем замену переменных

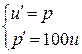(14.4)

и ставим начальные условия задачи Коши

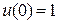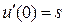; , (14.5)

где s - неизвестная константа, подлежащая определению.

Находим новые константы 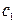и 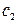из начальных условий (14.5).

Точное решение задачи Коши дается выражением

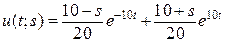, (14.6)

откуда видно, что значение u(1; s) очень чувствительно к изменению s.

Точное решение (14.3) краевой задачи получается при

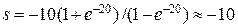. (14.7)

Если мы решим задачу Коши со значением s, определенным до двух десятичных знаков, скажем, при s = 9,99, то начиная с некоторого t* решение начнет расти к бесконечности. Значение t* вычисляется ниже.

Вследствие этого для получения хорошего приближения к решению краевой задачи требуется значительно более точное значение s.

Проблема, конечно, связана с тем, что решение задачи Коши растет, как 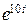и, чтобы подавить эту быстро растущую компоненту, начальное условие приходится определять очень точно.

В силу того, что в решении (14.3) есть растущая экспонента, это точное решение является неустойчивым относительно возмущения начального условия.

Действительно, рассмотрим возмущенное начальное условие:

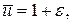0 < ε << 1,

(14.8)

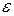- бесконечно малая величина

Тогда константа в (14.6) имеет вид:

, .

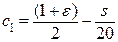При 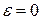решения 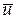естественно переходят в (14.6).

Вычислим

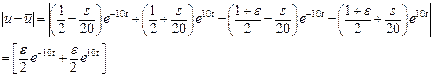
Однако никакая бесконечно малая величина 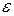не содержит роста экспоненты .

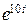Решение u(t) убывает, а затем при t > t 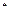растет. Значение t 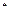определяется из необходимого условия экстремума:

,

, .

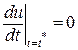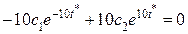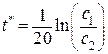Теперь применим метод Эйлера к системе (14.4) и получим систему разностных уравнений:

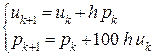(14.9)

В силу того, что известно точное решение, воспользуемся вторым замечательным пределом. Выберем .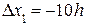

Решение этой системы разностных уравнений имеет вид

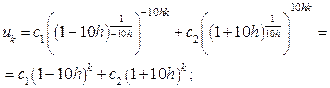
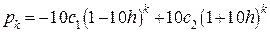. (14.10)

Первые слагаемые в (14.10) 1-10h < 1, что дает убывающую функцию. Второе слагаемое растет, т.к. 1+10h >1. Экспоненты здесь аппроксимируются степенными функциями.

Таким образом, с помощью решения неустойчивой задачи можно построить решение краевой задачи (14.1), если правильно подобрать s.

Дата добавления: 2015-05-26