
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 2. Предположим, что некоторому студенту пришла в голову мысль «подправить» метод Эйлера с целью, конечно
|
|
|
|
Предположим, что некоторому студенту пришла в голову мысль «подправить» метод Эйлера с целью, конечно, улучшить дело.
Рассмотрим многошаговый метод:

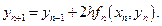 (12.23)
(12.23)
Сравним с методом Эйлера. Кажется, что замена шага h на 2h и сдвиг точки 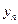 на один узел влево не дадут никаких последствий. Однако разберемся в этом, применив метод (12.23) к задаче:
на один узел влево не дадут никаких последствий. Однако разберемся в этом, применив метод (12.23) к задаче:
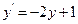 ,
, 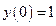 . (12.24)
. (12.24)
Разделим 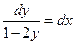 , интегрируем
, интегрируем 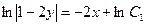 .
.
Тогда решение имеет вид
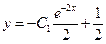 .
.
Определяем константу 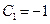 , тогда
, тогда
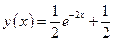 . (12.25)
. (12.25)
Проверим устойчивость по начальным данным. Рассмотрим возмущенную задачу
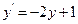 ,
, 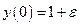 . (12.26)
. (12.26)
Найдем новую константу в общем решении 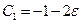 .
.
Получим решение:
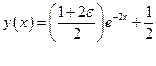 . (12.27)
. (12.27)
Функция экспоненциально убывает, следовательно, решение устойчиво и никаких «подводных камней» не видно.
Применим предлагаемый метод (12.23) к (12.24) и получим разностное уравнение:
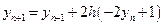 ,
, 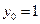 . (12.28)
. (12.28)
Применим теорию разностных уравнений к равенству (21.28), которое перепишем следующим образом:
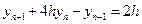 ,
, 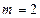 ,
, 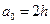 ,
, 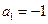 ,
, 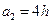 . (12.29)
. (12.29)
Соответствующее характеристическое уравнение 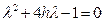 имеет корни
имеет корни

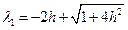 ,
, 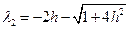 . (12.30)
. (12.30)
Таким образом, для решения уравнения (12.29) по формулам (12.14) - (12.16) получили представление
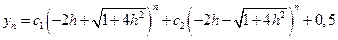 . (12.31)
. (12.31)
Оно позволяет легко определить поведение 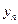 при
при 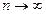 . Действительно, при любой фиксированной величине шага h > 0 очевидно, что
. Действительно, при любой фиксированной величине шага h > 0 очевидно, что
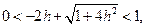
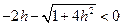 .
.
Следовательно, при 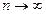 первое слагаемое в выражении (12.31) стремится к нулю, рассмотрим поведение второго слагаемого.
первое слагаемое в выражении (12.31) стремится к нулю, рассмотрим поведение второго слагаемого.
Возьмем, например, последовательность 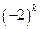 , где k = 1,N. Тогда имеет место последовательность: –2, 4, –8, 16, –31… Члены последовательности растут, меняя знак («скачут»), т.е. последовательность расходится. Аналогично ведет себя второе слагаемое. Так как точное решение (12.25) задачи (12.24) стремится к 0.5 при
, где k = 1,N. Тогда имеет место последовательность: –2, 4, –8, 16, –31… Члены последовательности растут, меняя знак («скачут»), т.е. последовательность расходится. Аналогично ведет себя второе слагаемое. Так как точное решение (12.25) задачи (12.24) стремится к 0.5 при 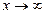 , ясно, что погрешность приближенного решения
, ясно, что погрешность приближенного решения 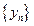 стремится к бесконечности и метод (12.23) в применении к задаче (12.24) оказывается неустойчивым. Подчеркнем, что этот рост погрешности никак не связан с ошибками округления, так как формула (12.31) является точным математическим представлением для
стремится к бесконечности и метод (12.23) в применении к задаче (12.24) оказывается неустойчивым. Подчеркнем, что этот рост погрешности никак не связан с ошибками округления, так как формула (12.31) является точным математическим представлением для 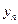 .
.
Приведенный пример ясно показывает, насколько важно, чтобы метод был в определенном смысле устойчивым. Определение устойчивости можно сформулировать [5] так:
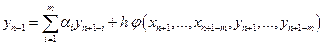 . (12.32)
. (12.32)
Метод (12.32) является устойчивым, если все нули 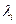 полинома
полинома

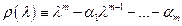 (12.33)
(12.33)
удовлетворяют условию 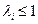 и любой нуль такой, что
и любой нуль такой, что 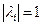 , является простым. Если в дополнение к этому m – 1 нулей полинома (12.33) таковы, что
, является простым. Если в дополнение к этому m – 1 нулей полинома (12.33) таковы, что 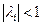 , то метод (12.32) является строго устойчивым.
, то метод (12.32) является строго устойчивым.
Любой метод, имеющий по крайней мере первый порядок точности, должен удовлетворять условию 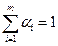 и, следовательно, l = 1 должно быть корнем соответствующего полинома (12.33). В этом случае для любого строго устойчивого метода полином (12.33) будет иметь один нуль, равный 1, а все остальные нули по абсолютной величине будут строго меньше, чем 1. Так как методы Рунге-Кутта являются одношаговыми, то для них
и, следовательно, l = 1 должно быть корнем соответствующего полинома (12.33). В этом случае для любого строго устойчивого метода полином (12.33) будет иметь один нуль, равный 1, а все остальные нули по абсолютной величине будут строго меньше, чем 1. Так как методы Рунге-Кутта являются одношаговыми, то для них 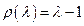 . Этот полином не имеет никаких других нулей, кроме
. Этот полином не имеет никаких других нулей, кроме 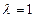 , и, следовательно, методы Рунге-Кутта всегда строго устойчивы. В случае m-шагового метода Адамса
, и, следовательно, методы Рунге-Кутта всегда строго устойчивы. В случае m-шагового метода Адамса 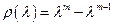 такого, что остальные m – 1 корней (12.33) равны нулю, такие методы также строго устойчивы.
такого, что остальные m – 1 корней (12.33) равны нулю, такие методы также строго устойчивы.
Для метода (12.29), рассмотренного в Примере 2, полином (12.33) принимает вид 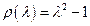 и имеет два нуля: +1 и –1. Следовательно, этот метод устойчив, но не строго устойчив. Именно отсутствие строгой устойчивости и приводит к неустойчивому поведению последовательности
и имеет два нуля: +1 и –1. Следовательно, этот метод устойчив, но не строго устойчив. Именно отсутствие строгой устойчивости и приводит к неустойчивому поведению последовательности 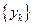 , порождаемой формулой (12.29). Это можно пояснить следующим образом. Разностное уравнение (12.29) имеет второй порядок (так как в него входят
, порождаемой формулой (12.29). Это можно пояснить следующим образом. Разностное уравнение (12.29) имеет второй порядок (так как в него входят 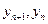 и
и 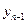 ) и, следовательно, имеет два фундаментальных решения
) и, следовательно, имеет два фундаментальных решения 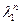 и
и 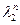 , где
, где 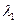 и
и 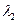 – корни характеристического уравнения, определяемые формулами (12.30). Последовательность
– корни характеристического уравнения, определяемые формулами (12.30). Последовательность 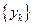 , получаемая по методу (12.29), строится с целью аппроксимации решения дифференциального уравнения первого порядка (12.24), которое имеет одно фундаментальное решение. Это фундаментальное решение аппроксимируется последовательностью
, получаемая по методу (12.29), строится с целью аппроксимации решения дифференциального уравнения первого порядка (12.24), которое имеет одно фундаментальное решение. Это фундаментальное решение аппроксимируется последовательностью 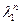 ; последовательность же
; последовательность же 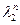 является «паразитной» и должна быстро стремиться к нулю, чего не происходит.
является «паразитной» и должна быстро стремиться к нулю, чего не происходит.
Однако 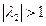 при любом h>0 и, следовательно,
при любом h>0 и, следовательно,  стремится к бесконечности, а не к нулю; именно это и вызывает неустойчивость. Заметим теперь, что при h
стремится к бесконечности, а не к нулю; именно это и вызывает неустойчивость. Заметим теперь, что при h  0 значения
0 значения 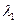 и
и 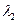 стремятся к нулям полинома устойчивости (12.24). Действительно, этот полином является предельным при h
стремятся к нулям полинома устойчивости (12.24). Действительно, этот полином является предельным при h  0 для характеристического полинома
0 для характеристического полинома 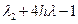 уравнения (21.19). Понятие строгой устойчивости теперь становится более очевидным. Если все, за исключением одного, нули полинома устойчивости по абсолютной величине меньше единицы, то при достаточно малом h все, кроме одного, корни характеристического уравнения рассматриваемого метода будут по абсолютной величине меньше единицы. Следовательно, степени этих корней, являющихся "паразитными" фундаментальными решениями разностного уравнения, будут стремиться к нулю и не приводить к возникновению неустойчивости.
уравнения (21.19). Понятие строгой устойчивости теперь становится более очевидным. Если все, за исключением одного, нули полинома устойчивости по абсолютной величине меньше единицы, то при достаточно малом h все, кроме одного, корни характеристического уравнения рассматриваемого метода будут по абсолютной величине меньше единицы. Следовательно, степени этих корней, являющихся "паразитными" фундаментальными решениями разностного уравнения, будут стремиться к нулю и не приводить к возникновению неустойчивости.
Теория устойчивости, которую мы только что обсудили, касается, по существу, устойчивости в пределе при h  0.
0.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 417; Нарушение авторских прав?; Мы поможем в написании вашей работы!