Вычисление производной

Понятие производной

Дифференцирование функции одной переменной

Упражнения

Найти пределы:

1)

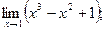
2)

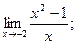
3)

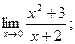
4)

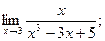
5) ;

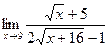6)

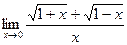
7) ;

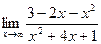8) ;

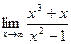9) ;

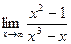10) ;

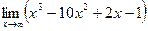11) ;

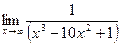12) ;

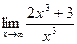13) ;

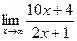14) ;

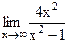15) ;

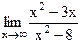16) ;

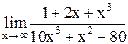17) ;

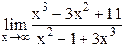18) ;

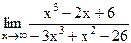19) ;

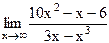20) ;

21) ;

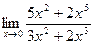22) ;

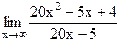23) ;

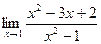24) ;

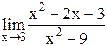25) ;

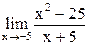26) ;

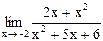27) ;

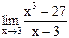28) ;

29) ;

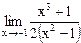30) ;

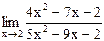31) ;

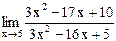32) ;

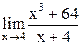33) ;

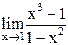34) ;

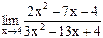35) ;

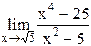36) ;

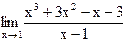37) ;

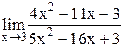38) ;

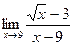39) ;

40) ;

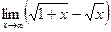41) ;

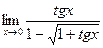42) ;

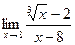43) ;

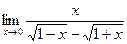44) ;

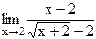45) ;

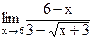46) ;

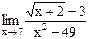47) ;

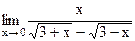48)

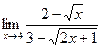
49) ;

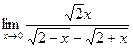50)

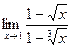
51) ;

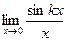52) ;

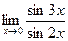53) ;

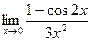54) ;

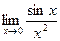55) ;

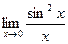56) ;

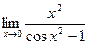57) ;

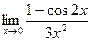58) ;

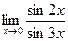59) ;

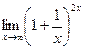60) ;

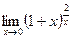61) ;

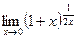62)

63) ;

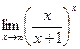64) ;

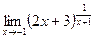65) ;

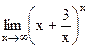66) ;

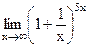67) ;

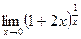Определение. Производной функции 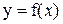в точке 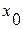называется предел при 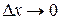отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).

Производная в точке 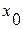обозначается 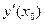или .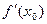

Итак, по определению производной имеем:

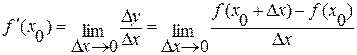
Процесс нахождения производной называется дифференцированием.

Геометрический смысл производной: для данной функции 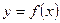ее производная 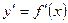для каждого значения 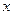равна угловому коэффициенту касательной к графику функции в соответствующей точке.

Физический смысл производной: для данной функции 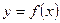, меняющейся со временем х, ее производная 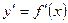есть скорость изменения функции y в данный момент времени х.

Правила дифференцирования:

1) Если функции u и v дифференцируемы в точке х₀, то их сумма дифференцируема в этой точке и

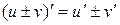
Примеры: 1) ;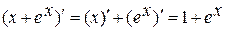

2) .

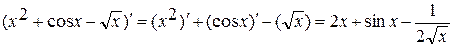(производная суммы рана сумме производных).

2) Если функции u и v дифференцируемы в точке х₀, то их произведение дифференцируемо в этой точке и

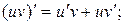
Примеры:

1) ;

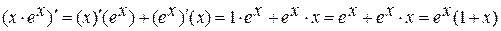2) .

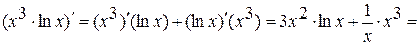
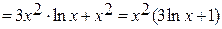3) Если функции u и v дифференцируемы в точке х₀ и функция v не равна нулю в этой точке, то частное 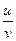также дифференцируемо в этой точке и ;

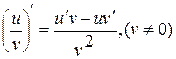Примеры:

1. ;

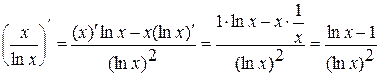2. .

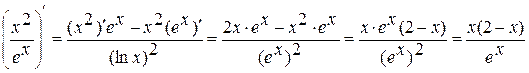4) В большинстве практических случаев процесс дифференцирования сводится к отысканию производной сложной функции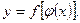

Если в цепи функциональных зависимостей 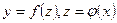аргумент х является последним, то мы будем называть его независимой переменной (чтобы подчеркнуть то обстоятельство, что изменение этого аргумента не зависит от поведения других переменных величин). Правило дифференцирования сложной функции вытекает из следующей теоремы.

Теорема. Есл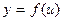и и 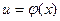– дифференцируемые функции от своих аргументов, то производная сложной функции 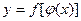существует и равна производной данной функции у по промежуточному аргументу и, умноженной на производную самого промежуточного аргумента и по независимой переменной x, т. е. .

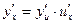Примеры:

1.

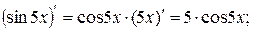
2.

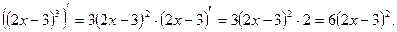
Дата добавления: 2015-06-26