Определенный интеграл. Определение определенного интеграла

Определение определенного интеграла.

Пусть функция 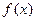определена на отрезке [a, b], a<b. Разобьем этот отрезок на n произвольных частей точками a=x₀<x₁<x₂<…<x_i-1<x_i<…<x_n=b. В каждом из полученных частичных отрезков [ x _i-1, x _i] выберем произвольную точку 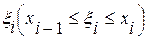и составим сумму

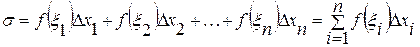(1)

где 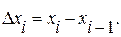Сумма вида (1) называется интегральной суммой для функции f(x) на [a, b].

Обозначим через l длину наибольшего частичного отрезка разбиения: .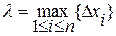

Определение. Если существует конечный предел I интегральной суммы (1) при 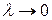, то этот предел называется определенным интегралом от функции f(x) по отрезку [a, b] и обозначается следующим образом:

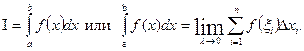
В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х – переменной интегрирования.

Для интегрируемости функции достаточно ее непрерывности на отрезке [a, b].

Основные свойства определенного интеграла.

1) По определению,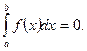

2) По определению,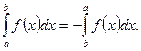

3) Каковы бы ни были числа a, b, c, всегда имеет место равенство

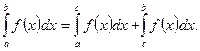
4) Постоянный множитель можно выносить за знак определенного интеграла, т. е.

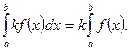
5) Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т. е.

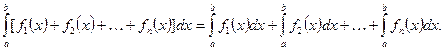
Дата добавления: 2015-06-26